Identification of Primary Factors Influencing Energy Consumption Patterns of Commercial and Residential Buildings
ⓒ 2020. KIEAE all rights reserved.
Abstract
Commercial and residential buildings are primary building types covering the majority of our built environment. Though, energy consumption pattern identification of those building types based on real-world data analysis has not been aggressively explored. Identification of primary factors influencing energy consumption patterns of commercial and residential buildings is the goal of this study.
CBECS and RECS data sets in the United States were used for commercial and residential building-energy-consumption pattern analysis. Multi-linear and seven machine learning algorithms are utilized to analyze building characteristics and end-use energy consumption patterns, e.g., cooling, heating, and water-heating. The SHAP value is utilized to describe influential factors in each energy consumption analysis model.
Ensemble algorithm yielded the lowest error rates compared with other algorithms. The calculated error rates also showed a lower level than the precedent studies performed on the CBECS and the RECS. Commercial building's cooling and heating energy consumption is more likely influenced by occupancy, while residential building's energy consumption is affected by equipment and climatic conditions. In the meantime, water-heating energy consumption shows noticeable dependency over the occupancy and climatic conditions for commercial and residential buildings. As a critical passive design element in the building, window has a more significant influence than overall insulation or roof finishing in identified residential buildings' energy consumption patterns.
Keywords:
Building energy consumption, Heating, Cooling, Water heating, SHAP values1. Introduction
1.1. Research background
Building energy performance is typically affected by outdoor conditions, building characteristics, occupants, and operational specifics. Due to this complexity, predicting building energy consumption is a difficult task to deal with[1-3]. More than a decade ago, Perez-Lombard et al.(2008) argued that available building energy information was insufficient and not proportional to its importance[4].
Amasyali and El-Gohary(2018) attempted a building-energy studies review. It was found that 47%, 31%, 20% and 2% of the examined studies were related to total, cooling, heating, and lighting energy prediction, respectively. On the other hand, Do and Cetin(2018) suggested to work on the residential-building energy-consumption prediction since residential buildings have received less attention. Less attention happened because of the limited availability of residential building data sets[3].
Furthermore, identifying key variables to construct a prediction model also becomes an essential task. Choi et al.(2017) performed a quantitative analysis based on energy consumption big data sets for residential buildings in Seoul, Korea[5]. Analysis performed with Pearson's correlation techniques showed that the correlation between electricity consumption and trading prices is higher than residential area and trading prices[5]. Kim et al.(2017) investigated the correlation between buildings and urban planning factors to identify significant variables on family-income groups[6].
In the meantime, the United States Energy Information Administration (EIA) has been administering the Commercial Building Energy Consumption Survey (CBECS) and the Residential Energy Consumption Survey (RECS) for nationally representative sample buildings. These surveys collect data sets related to building characteristics, energy sources, and energy usages[7][8].
1.2. Precedent studies
Previous studies based on CBECS and RECS (references[9]-[15]) are summarized in Table 1. Robinson et al.(2015) presented a comparison between using the least variables or common variables (total area, number of floors, HDD, CDD, and principal building activity) and extended variables. Results show that the extended variables model's MAE is lower than common features model one[11]. Noh et al.(2017) proposed a data cube model combined with association rule mining for analyzing the CBECS 2012 data sets. They harnessed C5.0 decision tree algorithm as an effective and powerful classification method to represent overall building characteristics into ten variables representing the most influential factors for identifying building energy consumption patterns[17]. Different from other studies, Troup et al.(2019) and Kim et al.(2018) studied building energy consumption prediction concerning windows[14][15].
As for identifying influential variables contributing to a certain outcome, regression coefficient calculation used to be a commonly used method. The percentage of mean square error (MSE) has also been used to detect critical variables. But, both of these methods only show a single numerical value to represent the relation between input and the output variables[12][13]. In the meantime, the latest approach in the domain of interpretable machine learning is using SHAP value as a method to describe the accuracy of model prediction based on Shapley value and local surrogate model[18].
1.3. Research objectives
Few studies have addressed the prediction modeling for residential building energy consumption and yet identifying influential variables is crucial for better understanding what variables determine observable energy consumption profiles in residential and commercial buildings. In this perspective, we performed analysis on commercial and residential building energy consumption patterns to find influential factors embedded in the CBECS and the RECS data sets utilizing SHAP value calculation. Through analyzing multiple years of survey data sets, we also tried to track down the differences between the 1990s and the 2010s in influential factors affecting building energy consumption. This research evaluated commercial and residential building energy consumption data sets with the following objectives:
a. How to predict energy consumption (cooling, heating, and water-heating) with higher accuracy based on selected features of different building types?
b. What variables could explain the differences between commercial and residential building energy consumption patterns based on each SHAP values?
c. What are the influential building energy-consumption factors of the 1990s compared to those of the 2010s?
To the best of our knowledge, this research is the first attempt to analyze the RECS data sets for residential building energy consumption prediction; compared influential variables for energy consumption predictions that embedded in the CBECS and the RECS data sets based on SHAP value as the variable significance indicator in such predictions.
2. Materials and methods
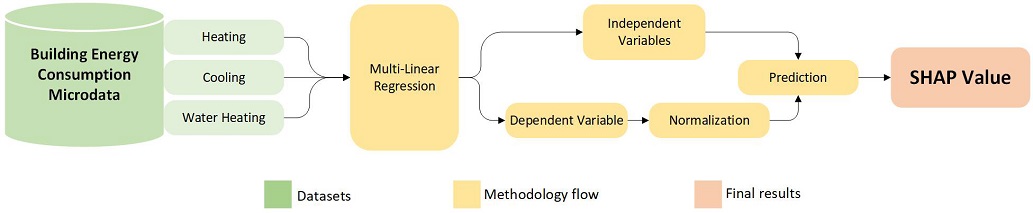
This research's overall framework is shown in Fig. 1. Each data set was classified into three different regression models based on the end-use energy consumption types (heating, cooling, and water-heating). Each model went through multi-linear regression to find significant variables/features based on each variable's p-value. Significant variables become candidate independent variables for the energy consumption prediction modeling based on selected machine learning algorithms. After this process, the variable importances were evaluated based on the SHAP value calculation. Among those variables that were turned out to be important in each data set, the comparisons were performed over the 1990s and the 2010s to find temporal changes reflected in significant variable set differences. The differences between the significant variables for commercial and residential building energy consumption predictions were also traced.
2.1. Commercial Buildings Energy Consumption Survey (CBECS) microdata
CBECS were conducted in two phases: building survey and energy supplier survey that non-energy related data sets were collected. The first CBECS was conducted in 1979, and the most recent one was the CBECS 2012[7]. In this research, we used the CBECS 1992 and the CBECS 2012. The CBECS 1992 included 6,734 buildings' data with 945 variables. Differently, 6,720 buildings' data and 1,120 variables were listed in the CBECS 2012. The detailed information for each variable are made available on the CBECS website[7].
2.2. Residential energy consumption survey (RECS) microdata
Like the CBECS, the RECS is also conducted through interviews to collect data on housing units' energy characteristics, energy usage patterns, and household demographics. With the latest RECS 2015, additional data from energy suppliers were added to estimate energy cost, usages for heating, cooling, appliances, and other end-users[8]. For this research, we used the RECS 1993 and the RECS 2015. The RECS 1993 includes 7,111 buildings' data with 826 variables, while the RECS 2015 contains 5,686 buildings' data with 760 variables. The detailed explanations for each variable are available on the RECS site[8].
2.3. Data processing
We performed a series of multi-linear regressions to explore influential variables as the potential KPIs(Key performance indicators) to predict building energy consumption and to identify each variable's significance level in each end-use energy consumption model[13]. The statistical significance for each end-use energy consumption model was tested using a p-value with α = 0.05; this test was done to all variables, including categorical variables, since those variables were also converted into numerical values.
Further analysis of the variables was done by calculating the missing values in each variable across all data sets. In this work, we took average value (for numerical variables) and mode value (for categorical variables) to impute each variable's missing values. Afterward, output or target data normalization was completed for each model to obtain higher accuracy. Data normalization was done through logarithmic transformation and exponential function was deployed to the numerical results as an antilog from the precedent normalization.
In this research, we tested seven different machine learning algorithms to predict building energy consumption profiles. Those algorithms were ridge regression, lasso regression, elastic net regression, support vector regressor (SVR), light gradient boosting machine (LightGBM), gradient boosting, and XGBoost [13][19]. Table 2. shows the hyperparameter value for those selected machine learning algorithms which include the constant (α), ElasticNet mixing parameter (L1_ratio), regularization parameter (C) and kernel coefficient (γ).
K-Fold cross-validation (kFold =10) were also performed for more accurate predictions. Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) were adopted as the error rate evaluation metrics.
2.4. SHAP value
Shapley additive explanation (SHAP) value is an indicator to interpret the prediction acquired through complex model algorithms which could explain individual variable. SHAP value is a combination between the Shapley value (which computes based on the cooperative game theory model) and the Local interpretable model-agnostic explanation (LIME) model (which focuses on training local surrogates to explain individual predictions)[18][20]. SHAP value has been proved to be consistent in both global and local interpretations.
We calculated the SHAP values by using the XGBoost algorithm to describe the influential factors. The twenty highest significant variables based on their SHAP value were plotted in the SHAP summary plot, which describes comparable importances of specific variables in each prediction instance.
3. Analytical results
3.1. Multi-linear regression analysis
CBECS and RECS data sets include a large number of variables. In order to reduce the number of variables, we performed a multi-linear regression analysis. Significant variables in the CBECS 1992, CBECS 2012, RECS 1993, and RECS 2015 were listed in Appendix A. Explanation of each variable is accessible on the EIA website[7][8].
3.2. Prediction metrics
Prediction metrics are described in Table 3., Table 4., and Table 5. Each building energy model was evaluated by calculating the average and the standard deviation of the evaluative metrics (RMSE and MAE) drawn from each fold, since 10 K-fold cross-validations were performed. Bold numbers in the tables indicate the lowest RMSE in each model, whereas italic numbers represent the lowest MAE in each model.

Prediction metrics for cooling energy analysis model (mean ± std. deviation calculated from each fold cross-validation)

Prediction metrics for heating energy analysis model (mean ± std. deviation calculated from each fold cross-validation)

Prediction metrics for water heating energy analysis model (mean ± std. deviation calculated from each fold cross-validation)
Table 3. shows the prediction results for the cooling model in both commercial and residential buildings. In commercial-building cooling-energy prediction (the CBECS 1992 and the CBECS 2012), the lowest RMSE and MAE are marked by either LightGBM, GradBoost, or XGBoost. Though, the lowest RMSE and MAE in residential cooling-energy prediction are made only by XGBoost.
Table 4. indicates prediction outcomes for the heating model. Similar to the cooling prediction case, the lowest RMSE and MAE for commercial heating-energy prediction were yielded by either LightGBM, GradBoost, or XGBoost. However, in the residential heating-energy prediction case, the lowest RMSE is marked by XGBoost, while GradBoost makes the lowest MAE.
Table 5. shows the prediction results for the water-heating model. The lowest RMSE and MAE for commercial water-heating-energy prediction were made by either LightGBM, GradBoost, or XGBoost. In this model, the lowest RMSE and MAE were generated by GradBoost.
Furthermore, the consistency of each model is evaluated through its standard deviation. As represented by the italicized numbers in Table 3., Table 4. and Table 5., most of lowest standard deviations were ascribed to the ensemble algorithm, XGBoost, specifically. In contrast with other data sets, regularization- regression (Lasso and ElasticNet) shows reliable performance with the RECS 2015 data set. In the cooling, heating, and water-heating RECS 2015 models, the lowest RMSE and standard deviation were generated by either Lasso or ElasticNet.
3.3. SHAP values in CBECS dataset
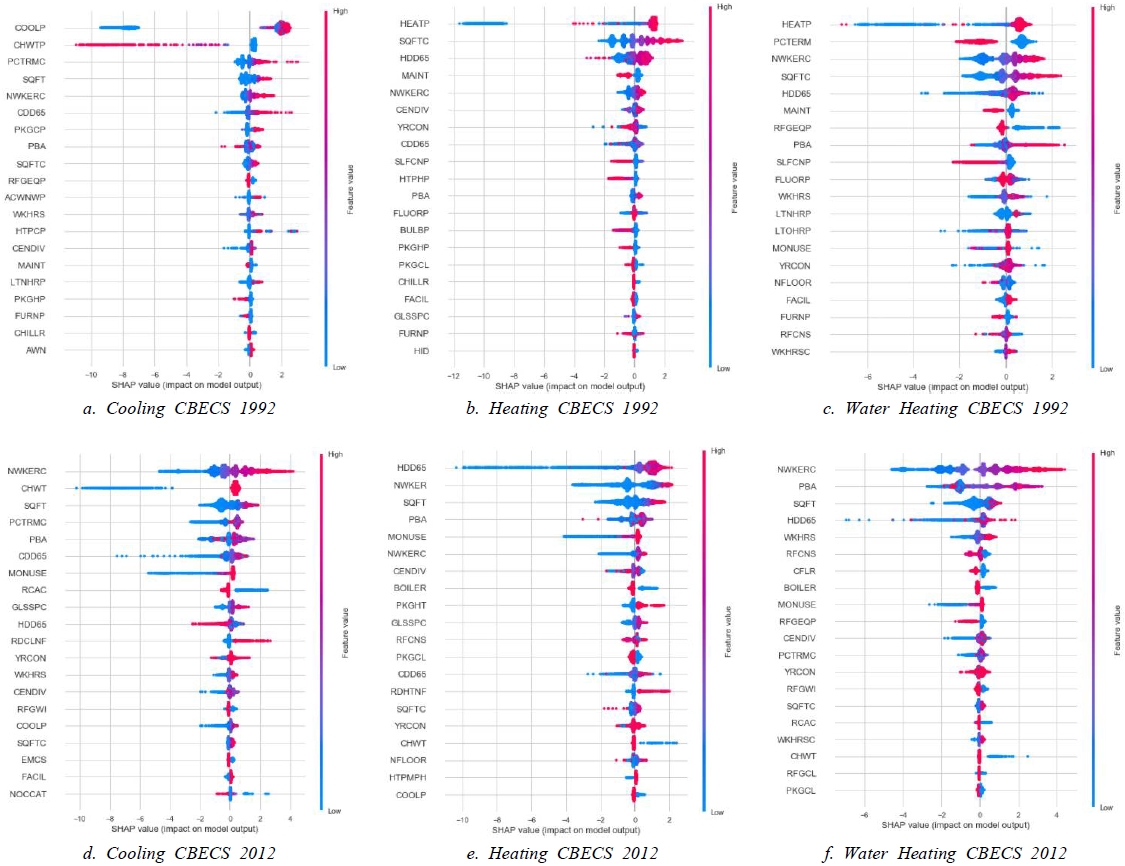
SHAP values are presented in summary plot graphs. In these plots, 20 variables that show the highest SHAP values are illustrated. For each variable, there are two outcomes for each evaluation point: SHAP value and variable value. SHAP value is defined by the positive or negative value on the x-axis, as shown in Fig. 2. and Fig. 3. Each dot's color defines the variable value, for instance pink color represents higher variable value whereas blue color indicates lower variable value.
Fig. 2. shows the SHAP summary plot for each end-use energy consumption model built upon CBECS data sets. With CBECS 1992 dataset, the cooling model illustrated in Fig. 2.(a) shows a set of influential variables including the highest five variables, namely, cooling percentage (COOLP), cooling percentage by district chilled water (CHWTP), number of computers (PCTRMC), total building area (SQFT), and number of workers category (NWKERC). CHWTP variable shows a negative correlation with cooling energy, which the higher value of CHWTP significantly reduces cooling energy consumption. PCTRMC, SQFT, and NWKERC variables show the same characteristics for commercial cooling energy consumption patterns; higher variable values induce higher positive SHAP value, impacting the corresponding model output. COOLP variable also shows a positive correlation, yet the lower value of COOLP would significantly generate a lower negative SHAP value than other CBECS 1992 variables.
Conversely, in the cooling model CBECS 2012 model shown in Fig. 2.(d), COOLP variables do not show the importance level as the same variable in the CBECS 1992 model. Instead, NWKERC marks the most significant variable in cooling-energy consumption in the CBECS 2012. District chill water (CHWT) also becomes one of the influential variable factors, which the lower value of CHWT (indicates district chilled water piped in) generates a negative correlation to cooling energy consumption. This evidence also supports the ground basis on CHWTP in the CBECS 1992.
The heating (Fig. 2.(b)) and water-heating (Fig. 2.(c)) model for CBECS 1992 data set share the same variables such as heating percentage (HEATP), total building area category (SQFTC), heating degree days (HDD65), number of workers category (NWKERC) and HVAC regular maintenance (MAINT). Other variables show a positive correlation to the heating and water heating model; while, the MAINT variable has the opposite tendency. A high variable value of MAINT (indicates no regular HVAC maintenance) would generate a lower negative SHAP value for heating and water-heating energy consumption. Surprisingly enough, in the water-heating model illustrated in Fig. 2.(c), computer usage (PCTERM) becomes one of the most significant variables. The high variable value of PCTERM (indicates computer usage in the building) also yields lower water-heating energy consumption. It is found that a higher PCTERM variable value indicated ‘No computer usage’ in the CBECS 1992 annotations. In fact, the absence of computer usage also indicated fewer workers (occupancy) in commercial buildings. This leads to lower water-heating energy consumption.
In the heating (Fig. 2.(e)) and water-heating (Fig. 2.(f)) model of CBECS 2012, NWKER (or NWKERC), HDD6, and SQFT were marked as common influential variables. Also, for the CBECS 2012, building activity importance level is higher than the CBECS 1992 case. It is also found that HDD65 variable value in CBECS 2012 (Fig. 2.(e) and 2.(f)) yields higher SHAP values than in the CBECS 1992 case ( Fig. 2.(b) and 2.(c)). The low variable value of HDD65 in the CBECS 2012 yields a more significant low negative-SHAP value than HDD65 in CBECS 1992 case.
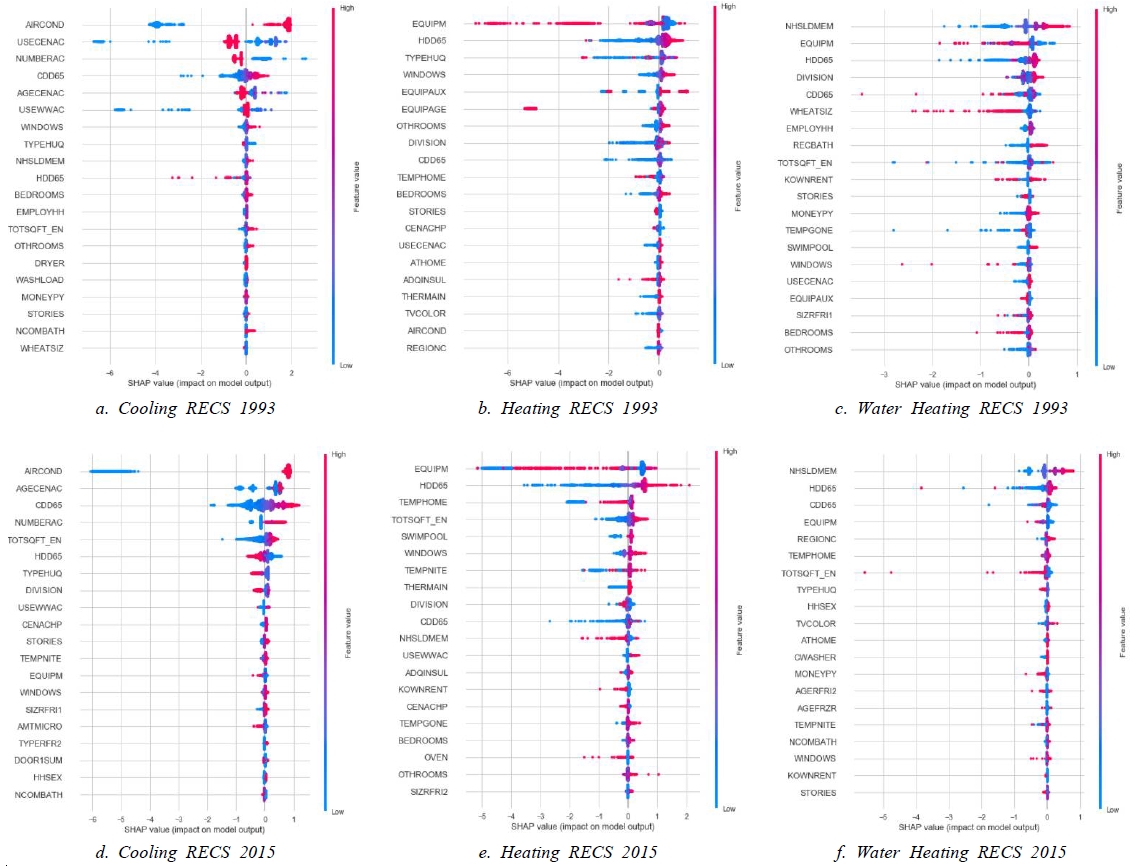
3.4. SHAP values in RECS dataset
Fig. 3. shows the SHAP summary plot for each end-use energy consumption model built upon RECS data sets. In Fig. 3.(a), the cooling-energy influential factors in the RECS 1993 are the usage of air-conditioning (AIRCOND), air-conditioning usage behavior (USECENAC), number of individual air-conditioning (NUMBERAC), cooling degree days (CDD65), and age of air-conditioning (AGECENAC). AIRCOND and CDD65 show a positive correlation with cooling energy consumption. Though, a higher variable value of NUMBERAC would generate the lower negative SHAP value. This case happens because RECS 1993 questionnaire put annotate '99' to indicate 'not applicable' choice for interviewees. The AGECENAC variable also has the same annotation as the NUMBERAC.
The bias annotation problem identified in RECS 1993 case is not repeated in RECS 2015 case; instead of annotating with the '99' for 'not applicable' choice, RECS 2015 annotates it with the '-2' value. Fig. 3.(d) shows SHAP values for RECS 2015 with the AIRCOND, AGECENAC, CDD65, and NUMBERAC are turned to be significantly influential variables.
Unlike heating and water-heating models built upon the CBECS dataset, heating and water-heating in RECS dataset do not share the same influential factors. The main space heating equipment type (EQUIPM) variable becomes the only common influential factor for heating and water-heating energy consumption in the RECS 1993 and RECS 2015.
In the heating model of RECS 1993 (Fig. 3.(b)), influential factors are EQUIPM, HDD65, type of housing unit (TYPEHUQ), number of windows (WINDOWS), secondary space heating (EQUIPAUX), and age of main space equipment (EQUIPAGE). HDD65, WINDOWS, and EQUIPAUX are positively correlated with heating energy consumption. In this model, bias annotations are also found in EQUIPAGE that yields pink dots in the lower negative SHAP values (Fig. 3.(b)).
In the heating model of RECS 2015, the EQUIPM, HDD65, and WINDOWS variables turn out to be influential factors (Fig. 3.(e)). Other than that, indoor-temperature related variables become influential factors such as daytime indoor home temperature during winter (TEMPHOME) and night time indoor home temperature during winter (TEMPNIGHT). Also, swimming pool ownership influences the heating energy consumption where a lower variable value (indicates not having a swimming pool) would generate a lower negative SHAP value. Housing unit variables also influence the heating energy consumption, such as total square footage (TOTSQFT_EN) that is positively related.
In the water-heating model of RECS 1993 (Fig. 3.(c)) and RECS 2015 (Fig. 3.(f)), there are some common influential variables in both years. The number of household members (NHSLDMEM), location (census region (REGIONC) and census division (DIVISION)), EQUIPM, CDD65, and HDD65 are those common influential factors in both years. Interestingly, this is the only model that yields both CDD65 and HDD65 as influential factors. CDD65 is the factor that negatively correlated with water-heating energy consumption. On the other hand, HDD65 is positively correlated with water-heating energy consumption.
In addition to the water-heating model of RECS 2015 (shown in Fig. 3.(f)), TEMPHOME variable is an influential one even though it is not so significant. The total building area (TOTSQFT_EN) variable in the water-heating model also significantly impacts water-heating energy consumption. A high variable value of TOTSQFT_EN would significantly lower water-heating energy consumption (Fig. 3.(f)). In contrast, the low variable value of TOTSQFT_EN in the RECS 1993 scatters along with the SHAP value without any trends detected (shown in Fig. 3.(c)).
4. Discussion
Machine-learning-based building-energy consumption predictions with SHAP value calculation were performed to identify the most influential factors impacting energy consumption and the differences reflected by survey years and building types. Results show that the ensemble algorithms possess advantages in lowering both RMSE and MAE. These results also confirm the outcome of a previous study by Robinson et al.(2015)[11]. We also found that RMSE and MAE that are marked in this study show the lowest error rate than other precedent studies.
Regarding its consistency, we also identified that the ensemble algorithm has better consistency than other algorithms. Meanwhile, in the RECS dataset, the regularization-regression algorithm (Lasso and ElasticNet) shows fairly reliable performance in error rate and standard deviation. We could infer that the regularization-regression algorithm could work well on a complete dataset since there is no missing data on the RECS 1993 and RECS 2015.
As being reflected on SHAP values, influential factors on energy consumption are also revealed. Table 6. shows the findings on the variables’ trend differences in each energy model. Lokhandwala et al.(2018) found that the CBECS 2012 cooling-energy consumption increases as a function of non-climatic conditions relative to the CBECS 2003[12]. In reference to that statement, our study revealed that neither CDD65 nor HDD65 is marked as the source for the highest cooling-energy SHAP value. Fig. 2.(d) shows that the lower value of CDD65 in the CBECS 2012 significantly decreases cooling-energy consumption compared to CDD65 in CBECS 1992, which only slightly impacts the output.
The comparisons of SHAP values between the 1990s data set and the 2010s data set give some fascinating insight. Based on the heating energy model of RECS 2015, a higher number of household members (NHSLDMEM) would decrease heating energy consumption, which did not happen in the RECS 1993. Also, in the RECS 1993, square footage (TOTSQFT_EN) was positively related to water-heating energy consumption, which means a more extensive building area would consume more. Reversely, TOTSQFT_EN was negatively related to water-heating energy consumption in the RECS 2015. In addition, Fig. 2. shows that the number of worker factors in the CBECS 2012 becomes more influential than its SHAP values in the CBECS 1992.
In commercial buildings, common variables that influence cooling and heating energy consumption are the number of workers and the occupancy variables. On the other hand, residential energy consumption is more influenced by its HVAC appliances and climatic conditions. Only residential water-heating energy consumption is significantly influenced by NHSLDMEM. Furthermore, we also identified that residential buildings' windows are more influential than other passive design factors (i.e., insulation and roof).
5. Conclusion
This study investigated commercial and residential building-energy consumption prediction models based on the CBECS and the RECS data sets collected in the United States. Several selected machine learning algorithms were tested and acquired outstanding error rate reduction compared with precedent studies. SHAP value was also utilized to illustrate influential factors for building energy consumption. Influential factors such as climatic condition and occupancy show differences in commercial and residential buildings between the 1990s and the 2010s.
A more significant influence of climatic conditions is expected in future years. The number of workers in the 2010s also increasingly influence energy consumption in commercial buildings compared with the 1990s. Commercial buildings' cooling and heating energy are highly influenced by occupancy patterns based on our study, while residential buildings' cooling and heating energy are highly affected by equipment and climatic conditions. In the meantime, water-heating energy consumption is influenced by occupancy and climatic condition in both commercial and residential buildings.
In this research, we limited our study to CBECS and RECS data sets considering the data sets' data availability and size. Further study might need to relate the results inferred from the calculated SHAP values with various social and economic conditions. This process would strengthen the merit for machine-learning-based building-energy consumption prediction and stimulate potential beneficiaries to guarantee more informed and controlled energy consumption behaviors in the future based on climatic, social, and economic dimensions.
Acknowledgments
This work is supported by the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure, and Transport (Grant 20PIYR-B153277-02).
This work is also supported by Smart City R&D project of the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant 20NSPS-B150126-03).
References
-
H. Zhao and F. Magoulès, A review on the prediction of building energy consumption, Renew. Sustain. Energy Rev., 16(6), 2012, pp. 3586–3592.
[https://doi.org/10.1016/j.rser.2012.02.049]

-
K. Amasyali and N. M. El-Gohary, A review of data-driven building energy consumption prediction studies, Renew. Sustain. Energy Rev., vol. 81, 2018, pp.1192–1205.
[https://doi.org/10.1016/j.rser.2017.04.095]

-
H. Do and K. S. Cetin, Residential Building Energy Consumption: a Review of Energy Data Availability, Characteristics, and Energy Performance Prediction Methods, Curr. Sustain. Energy Rep., 5(1), 2018, pp.76–85.
[https://doi.org/10.1007/s40518-018-0099-3]

-
L. Pérez-Lombard, J. Ortiz, and C. Pout, A review on buildings energy consumption information, Energy Build., 40(3), 2008, pp.394–398.
[https://doi.org/10.1016/j.enbuild.2007.03.007]

-
최준우 외 4인, 주거용 건물의 에너지 실사용량의 불확실성을 내포한 설명변수 인자에 대한 빅데이터 분석 기반의 정량화 방법-서울지역의 공동주택을 중심으로J, 생태환경건축학회지, 17(3), 2017, pp.75-81.
J. W. Choi et. al., The Method of Quantitative Analysis Based on Big Data Analysis for Explanatory Variables Containing Uncertainty of Energy Consumption in Residential Buildings : Focused on Apartment in Seoul Korea, KIEAE Journal, 17(3), 2017, pp.75–81. [https://doi.org/10.12813/kieae.2017.17.3.075]
-
김기중, 안영수, 이승일, 소득격차를 고려한 조건에서 건물과 도시계획 요소가 건물에너지 소비에 미치는 영향요인 분석, 국토계획, 52(5), pp.253–267, 2017.
K.J. Kim, Y.S. An, S.I. Lee, Analysis of Influencing Factors of Building and Urban Planning on Building Energy Consumption Considering Income Gap – Focused on electricity consumption on August in Seoul, Journal of Korea Planning Association, 52(5), 2017, pp.253–267. [https://doi.org/10.17208/jkpa.2017.10.52.5.253]
- Energy Information Administration (EIA)- Commercial Buildings Energy Consumption Survey (CBECS), https://www.eia.gov/consumption/commercial/, (accessed Jun. 11, 2019).
- Residential Energy Consumption Survey (RECS) - Energy Information Administration, https://www.eia.gov/consumption/residential/index.php, (accessed Jun. 11, 2019).
-
M. Yalcintas and U. Aytun Ozturk, An energy benchmarking model based on artificial neural network method utilizing US Commercial Buildings Energy Consumption Survey (CBECS) database, Int. J. Energy Res., 31(4), 2007, pp.412–421.
[https://doi.org/10.1002/er.1232]

- A. Kaskhedikar, T. A. Reddy, and G. Runger, Use of random forest algorithm to evaluate model-based EUI benchmarks from CBECS database, ASHRAE Trans., 121(1), 2015, pp.17-28.
-
C. Robinson et al., Machine learning approaches for estimating commercial building energy consumption, Appl. Energy, vol. 208, 2017, pp.889–904.
[https://doi.org/10.1016/j.apenergy.2017.09.060]

-
M. Lokhandwala and R. Nateghi, Leveraging advanced predictive analytics to assess commercial cooling load in the U.S., Sustain. Prod. Consum., vol. 14, 2018, pp.66–81.
[https://doi.org/10.1016/j.spc.2018.01.001]

-
H. Deng, D. Fannon, and M. J. Eckelman, Predictive modeling for US commercial building energy use: A comparison of existing statistical and machine learning algorithms using CBECS microdata, Energy Build., vol. 163, 2018, pp.34–43.
[https://doi.org/10.1016/j.enbuild.2017.12.031]

-
L. Troup, R. Phillips, M. J. Eckelman, and D. Fannon, Effect of window-to-wall ratio on measured energy consumption in US office buildings, Energy Build., vol. 203, 2019, p.109434.
[https://doi.org/10.1016/j.enbuild.2019.109434]

-
S. Kim and E. Shim, Statistical Analysis of Window Impacts on Cooling and Heating Energy Use in Single Family Residence Based on Climate Regions in U.S.A., KIEAE Journal, 18(6), 2018, pp.5–11.
[https://doi.org/10.12813/kieae.2018.18.6.005]

-
P. A. Mathew, L. N. Dunn, M. D. Sohn, A. Mercado, C. Custudio, and T. Walter, Big-data for building energy performance: Lessons from assembling a very large national database of building energy use, Appl. Energy, vol. 140, 2015, pp.85–93.
[https://doi.org/10.1016/j.apenergy.2014.11.042]

-
B. Noh, J. Son, H. Park, and S. Chang, In-Depth Analysis of Energy Efficiency Related Factors in Commercial Buildings Using Data Cube and Association Rule Mining, Sustainability, 9(11), 2017, p.2119.
[https://doi.org/10.3390/su9112119]

- S. M. Lundberg and S.-I. Lee, A Unified Approach to Interpreting Model Predictions, in Advances in Neural Information Processing Systems 30, Long Beach, 2017, p.10.
- J. Han, M. Kamber, J. Pei. Data Mining Concepts and Techniques, 3rd ed., Massachusetts: Morgan Kaufmann, 2012.
- C. Molnar. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable, https://christophm.github.io/interpretable-ml-book/, , 2020.