Utilization and Verification of Inverse Distance Weighting (IDW) Interpolation Technology for Predicting Solar Radiation of Photovoltaic System
ⓒ 2022. KIEAE all rights reserved.
Abstract
Weather conditions around solar photovoltaic (PV) systems have a direct effect on the amount of generated power. Therefore, highly correlated meteorological environmental variables are used to accurately predict the power generation capacity of PV systems. However, it is difficult to install observation equipment due to high installation costs and maintenance. Therefore, public data from the Korea Meteorological Administration are often used. However, uncertainty may arise due to the large distance between the stations of the Korea Meteorological Administration. Therefore, in this study, inverse distance weighting (IDW) was used to predict the solar radiation of an arbitrary area to improve the uncertainty caused by the large distance between the meteorological stations.
In this study, IDW was used as a spatial statistical technique to predict the monthly average of daily accumulation solar radiation in South Korea. Moreover, four cases of the automated synoptic observing system (ASOS) were used as study cases to evaluate the prediction technology. The actual solar radiation observed and the predicted solar radiation was compared and analyzed in each study case, and the accuracy was evaluated as an indicator of the mean absolute percentage error (MAPE). Additionally, the MAPE was compared with the prediction results of the multiple regression model.
Although the results differ for each case, the average MAPE was approximately 11.06% using the inverse distance weighting interpolation method, and the predicted value by the multiple regression method yielded an average MAPE of approximately 16.12%.
Keywords:
Solar Radiation, Inverse Distance Weighted Method, Photovoltaic System, Interpolation1. Introduction
1.1. Background and Purpose of the Study
Predicting the amount of solar power generation is pivotal for the rational design of optimal capacity, equipment selections, and investment and feasibility analyses of related projects. In general, the meteorological elements at the location of the PV power system constantly change while the power generation facility is operational, which directly impacts the estimation of the amount of power generation of a PV system[1]. Hence, several meteorological elements highly correlated with power generation have been used to accurately predict power generation[2]. Ideally, meteorological data measured at the location of the PV power plant should be used to develop a highly accurate model to predict power generation. However, it is practically difficult to install meteorological observation equipment at all potential locations of PV power generators and systems. In particular, compared to the temperature or humidity sensing, it is rare to install observation equipment to measure solar radiation closely linked with PV power generation owing to high cost, sophisticated installation technology, sensor calibration, and regular maintenance[3].
Consequently, the public data provided by the National Climate Data Center of the Korean Meteorological Administration, such as the Automated Synoptic Observing System (ASOS) and Automatic Weather System (AWS), can be used in such cases. However, when there is a large distance between the Korean Meteorological Administration stations, it becomes difficult to identify the meteorological factors in areas without installed weather. In particular, solar radiation, which is a fundamental factor that affects PV power generation, is measured only at 44 ASOSs in Korea with an average distance of 205.7km among the 44 ASOSs. In other words, the distance between the stations can result in uncertainties when the amount of power generation is estimated at potential locations of a PV power generation system using the weather factors observed at the meteorological stations of the KMA.
Hence, a more accurate prediction of meteorological factors is needed in areas without any installed meteorological stations . In this study, inverse distance weighting (IDW) is used as a spatial statistical method to improve the accuracy limit of the power generation prediction resulting from the large distance between the weather stations by estimating the solar radiation in the potential areas of a meteorological station.
IDW interpolation is a method to estimate the values at a location of interest by using the data observed from multiple nearby points[4]. Unlike machine learning and statistical modeling, which require a benchmark data set of the location of interest, the IDW method only uses the data from nearby points, making it ideal for predicting the solar radiation at a potential location of a PV system.
1.2. Method and Scope of the Study
In this study, the IDW method is used as a spatial statistical technique to predict solar radiation of a specific location. Subsequently, the applicability of the prediction technique for the analysis target is evaluated by considering four ASOSs in Korea.
The accuracy of the spatial statistical technique was evaluated by comparing and analyzing the measured and the predicted solar radiation from the analysis targets. The solar radiation and meteorological factors of the analysis targets were used to develop a multiple regression model, and the values predicted by the model were compared with the solar radiation estimated by the spatial statistical technique to verify the effectivity of the IDW technique.
2. Interpolation and Prediction Methods
2.1. Inverse Distance Weighted Method (IDW)
Inverse distance weighting (IDW) is used to predict the desirable values of a specific location without an observatory (randomly selected areas) by using the coordinates obtained from observation points. It is an analytical approximation to estimate values among the points using the mathematical characteristics of space. The estimation of the values can be based on the investigated impact of a coordinate of an unknown observatory on the coordinate of the other unknown observatory and the values that decrease with the distance between an unknown observatory and the existing observatory. Accordingly, a relatively larger weight is placed on the observatory of a closer distance to determine the value of the interpolation point.
The IDW method is used widely in a variety of research and practice areas owing to its simplicity among spatial statistical analysis methods[5]. It can be expressed as Eq.1 to spatially interpolate irregular spatial information in a two-dimensional (2D) space using a computer mapping program[6].
| (Eq. 1) |
where Z denotes the predicted value of the prediction point, Zi represents the reference value of the location (xi,yi), Wi indicates the weight, di corresponds to the distance between the target grid point and the observation point, b symbolizes the distance weighting factor, and n denotes the number of reference values. Here, the greater the distance weighting factor b, the lesser the impact of the data at a further distance from the target area. Commonly, b=2 is used in the process[7].
In this study, the GIS program (QGIS) was used to implement the IDW method, and the weighting factor b was set at 2 and the interpolation pixel range was 129 × 122 pixels. The size of the pixel was set to 5,000m × 5,000m, and the solar radiation estimated with a resolution of 5 km was analyzed.
2.2. Multiple Regression Analysis
Multiple regression is a statistical analysis method used to predict target variables from independent variables with the regression equation derived by analyzing the functional relationships between variables. The relationship between the dependent variable (y) and the independent variable (x1, ···, xn) is shown in Eq. 2.
| (Eq. 2) |
Here, y denotes the target variable, β0,β1,⋯,βn denote the regression coefficients associated with independent variables, εk represents the residual, xnk corresponds to an independent variable value for independent variable n with k observation points.
In the present study, Pearson correlation analysis of the independent variables was performed in relation to the target variables to develop a multiple regression model. The daily accumulated solar radiation is the target variable of the regression model, and the meteorological variables observed at the ASOS constitute the independent variables. Among the meteorological variables observed at the ASOS, sunshine hours (0.83), cloudiness (-0.56), relative humidity (-0.38), temperature (0.33), and precipitation (-0.32) were found to be correlated with the target variables. Hence, a multiple regression model was developed using the meteorological variables as an independent variable. The multiple regression model is shown in Eq. 3.
| (Eq. 3) |
Here, y denotes the predicted solar radiation, x1 represents the sunlight hours, x2 indicates cloudiness, x3 corresponds to the relative humidity, x4 is used to represent the temperature, x5 resembles the precipitation, and the determination coefficient (R2) was found to be 0.80.
Meanwhile, if there are correlations between variables, the explanatory power of independent variables can be interfered due to multicollinearity, resulting in serious problems in the validity of the regression model[8]. Therefore, the variance inflation factor (VIF) representing the degree of expansion of the variance was examined to ascertain if it is 10 or less, and it was found that the variance inflation factor for all variables was less than 5, confirming that there is no issue of multicollinearity.
3. Data Collection and Analysis Target
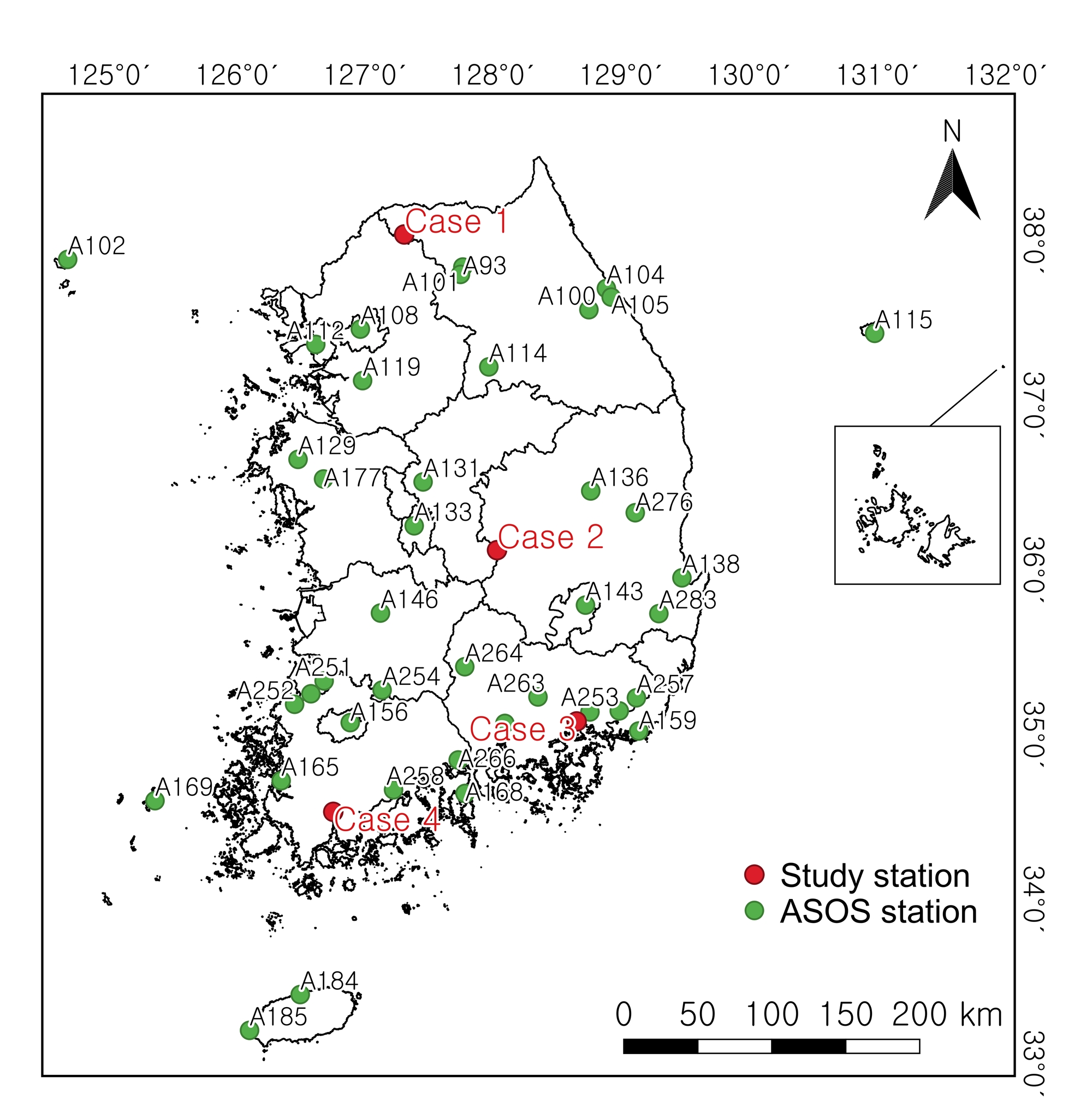
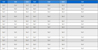
In this study, IDW was performed using the data collected from the ASOS of the ground observatory among the KMA’s weather stations. In total, 102 ASOSs of the KMA are in operation, and 44 of them measure solar radiation. Thus, 40 stations were used to perform the IDW and multiple regression models, and four randomly extracted observatories were set as verification and analysis targets. Fig. 1. illustrates the locations of 44 ASOSs where solar radiation is observed. Moreover, detailed information of the four observatories is listed in Table 1.
The analysis used meteorological data, which included the daily accumulated solar radiation observed at the ASOSs, daily temperature, precipitation, wind speed, relative humidity, sunshine hours, and cloudiness, and the monthly average calculated from the daily accumulated solar radiation used. The data were collected from April 2019 to March 2020, and the data were obtained through the open MET data portal (data.kma.go.kr).
4. Analysis and Results
The IDW method was employed to predict the solar radiation of an area without any installed observatories and observed values. Moreover, the observed data was analyzed and compared with the values predicted using the multiple regression model to verify the IDW method. The accuracy of prediction was evaluated by the mean absolute percentage error (MAPE), which can be calculated as shown in Eq. 4.
| (Eq. 4) |
The monthly average of the daily accumulated solar radiation observed from April 2019 to March 2020 was estimated using the IDW method and the contour map of the estimated monthly solar radiation in Korea is shown in Fig. 2. The solar radiation prediction map was drawn up by the resolution of 5km × 5km with the poles (eastern, western, southern, and northern ends) of the Korean territory as the boundary, and the estimates of 129 × 122 pixels (15,738 pixels) were obtained.
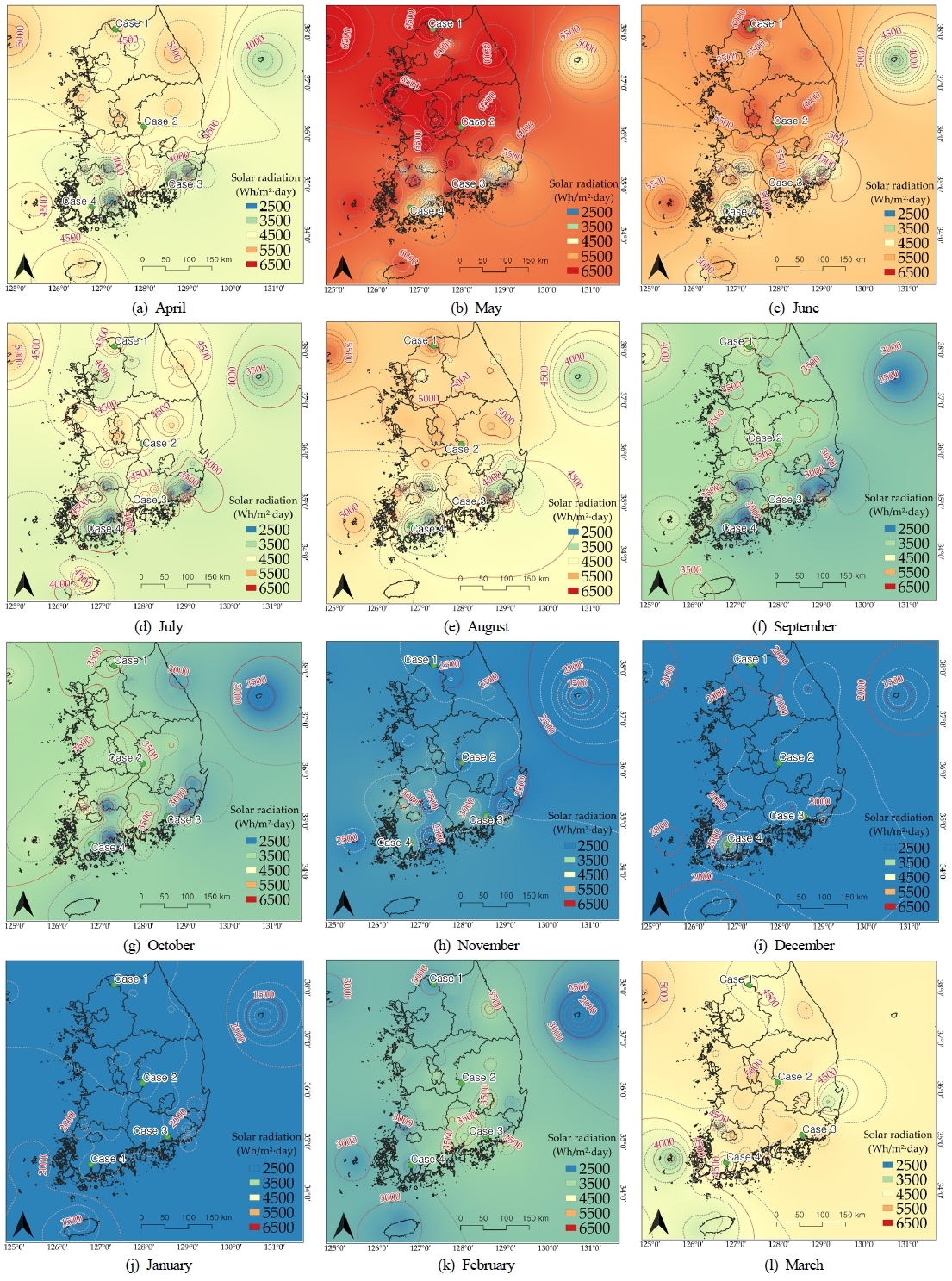
Contour map of the estimated monthly average of daily accumulation solar radiation by IDW from April 2019 to March 2020, (a)-(l)
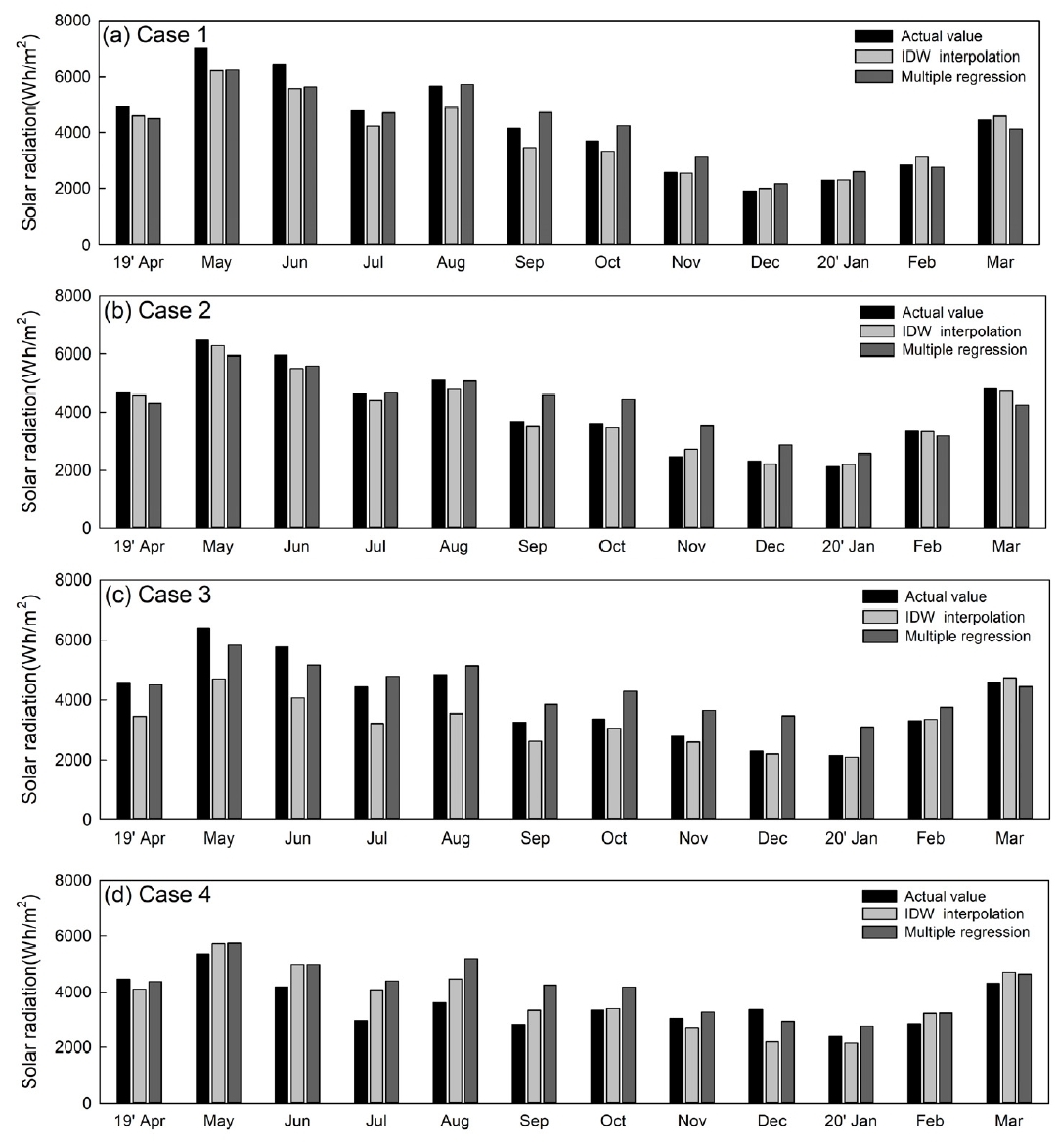
It was found that the daily accumulated solar radiation in Korea determined by the contour map increased in the spring. Generally, it exhibited a range of approximately 5,500Wh/m2·day and an even higher range in May and June. Meanwhile, the solar radiation exhibited a downwards trends after September (during autumn), and it fell to 2,500Wh/m2 and lower during the winter months from November to January. Furthermore, as for the regional trends identified by the contour map, the amount of solar radiation near the Gyeongsangnam-do coast in the Southern region, Jeollanam-do coast, Jeollabuk-do inland area (near Sunchang), and Ulleung-do was relatively lower than other regions, even in the same period or month. Meanwhile, the estimated solar radiation of the four points selected as the study case in the contour map was investigated using the pixel values corresponding to the location of each case. In addition, the amount of solar radiation estimated by the multiple regression model was calculated using Eq. 3 and the meteorological data (sunshine hours, cloudiness, relative humidity, temperature, and precipitation) observed at the study case weather stations. Consequently, the solar radiation estimated by the IDW interpolation and multiple regression models for each study case is depicted in Fig. 3., and the MAPE that represents the accuracy of prediction was analyzed as presented in Table 2.
With regards to the predicted values and accuracy for each case, the observed solar radiation of the Case exhibited an increasing tendency in spring and a declining trend in winter with the range of 1,892.8~7,035.9Wh/m2·day on a monthly basis. Moreover, the predicted values obtained by the IDW interpolation, and the multiple regression model exhibited a similar tendency to the observed values in the range of 1,990.6~6,225.6Wh/m2·day and in the range of 2,163.3~6,242.3 Wh/m2·day, respectively.
The MAPE for the predicted solar radiation was found to have an average of 8.70% for 12 months using the IDW method, indicating high accuracy of less than 10%. However, as for the monthly accuracy, the MAPE was found to have a maximum of 16.59% in September, though it exhibited an exceedingly high accuracy of the minimum of 0.84% in November. Moreover, the MAPE of the multiple regression model was 10.29%, approximately 1.59% higher than that of the IDW, and the monthly accuracy exhibited a high level of accuracy of the minimum 1.17% in July while it exhibited an accuracy of 21.97% in November, indicating a considerable difference between monthly accuracies.
Case 2 exhibited a similar trend as Case 1 in terms of the observed solar radiation in the range of 2,135.9~6,469.5 Wh/m2·day. The yearly solar radiation estimated using the IDW varied in the range of 2,214.9~6,274.6Wh/m2·day, and the yearly solar radiation estimated using the multiple regression model varied in the range of 2,554.1~5,946.1Wh/m2·day.
In Case 2, the 12-month average MAPE for the estimated solar radiation was found to be 4.27% by the IDW and 14.46% by the multiple regression model, respectively. In particular, the accuracy by the IDW was found to exhibit a high accuracy of less than 5%, indicating the highest accuracy among the analysis targets at the four points. Compared to the MAPE obtained by the multiple regression model of 14.46%, it exhibited a lower error rate of approximately 10.2%, indicating that it is the case with the highest prediction performance of the IDW.
For Case 3, the monthly average of daily accumulated solar radiation tended to increase in spring and decrease in winter in the range of 2,159.2~6,404.8Wh/m2·day. Meanwhile, the predicted values obtained by the IDW interpolation and the multiple regression model were found to vary in the ranges of 2,095.4~4,741.81Wh/m2·day and 3,123.4~5,827.3Wh/m2·day, respectively.
At that point, the 12-month average accuracy of the value estimated by the IDW was discovered to be 15.15%, and it was 18.56% when estimated using the multiple regression model, indicating that the accuracy of Case 3 was relatively lower than that of Case 1 and Case 2. In particular, the MAPE estimated using IDW was found to be an average of 25.58% in the spring and summer months of April to September when the solar radiation was high. Meanwhile, the MAPE estimated using the multiple regression model exhibited a very high average accuracy of 38.32% in the autumn and winter months between October and January when the solar radiation was low, indicating that the two prediction models exhibited opposite seasonal tendencies.
In Case 4, the observed solar radiation ranged from 2,403.2 to 5,355.8Wh/m2·day, whereas the solar radiation estimated using IDW was in the range of 2,137.9~5,735.5Wh/m2·day and the solar radiation predicted using the multiple regression model was in the range of 2,779.1~5,754.6Wh/m2·day. In particular, the difference between the maximum and minimum observed solar radiation of Case 4 was 2,952.6Wh/m2·day on average, approximately 1,620.4Wh/m2·day lower than that of Cases 1, 2, and 3 of an average of 4,573Wh/m2·day, indicating that the annual solar radiation range was relatively narrow at the location of Case 4.
In Case 4, the MAPE estimated using the IDW indicated a large deviation from month to month, with a minimum of 1.74% in October and a maximum of 36.87% in July. Moreover, the annual average MAPE was found to be 16.10%, confirming that Case 4 had the largest prediction error among the four study cases. In addition, the MAPE of solar radiation predicted using the multiple regression model was low at 1.75% in April but exceedingly high at 50.09% in September, indicating a significant deviation by month, and the 12-month average was also found to be high as 20.94%.
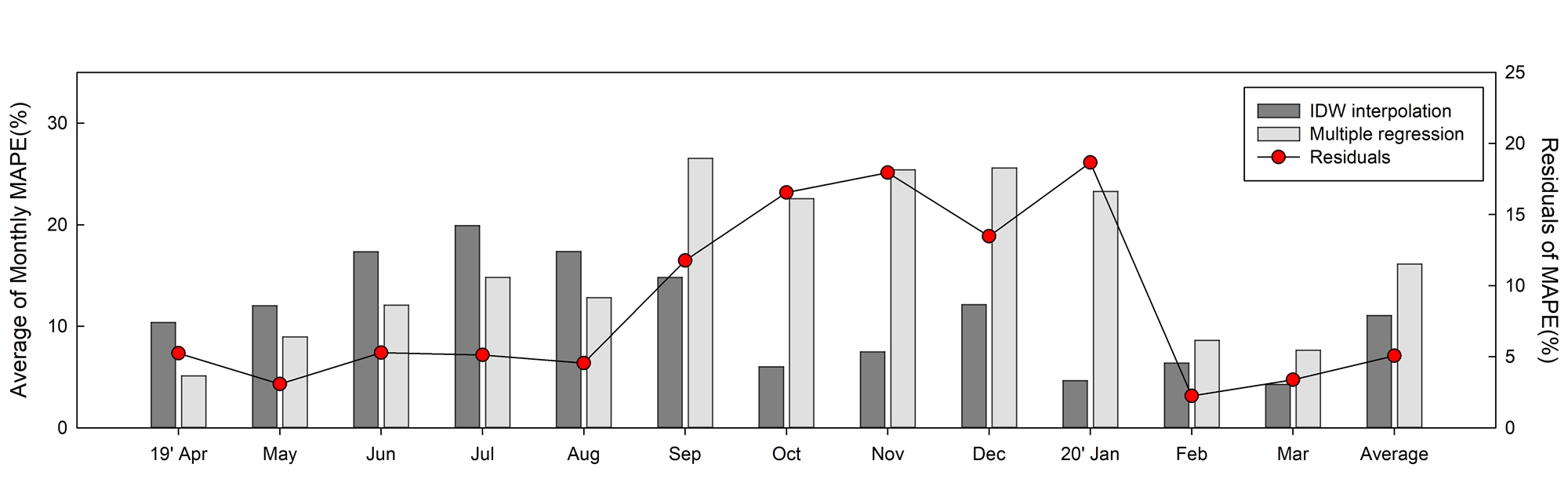
In summary, an average of approximately 11.06% of MAPE was obtained by the IDW, though it varied by case. Meanwhile, the predicted value using the multiple regression model yielded an average MAPE of approximately 16.12%, indicating that the prediction results of the IDW were approximately 1.46 times more accurate than that of the multiple regression model. However, when the accuracy was identified for each case, the monthly difference between the maximum and minimum accuracy was found to be large. Therefore, evaluating the two prediction models with the 12-month average MAPE is unreasonable.
Accordingly, as shown in Fig. 4., the monthly average prediction accuracy of both the IDW interpolation and the multiple regression model for the four study cases were compared and analyzed. Resultantly, the IDW was found to be rather inaccurate, primarily because the MAPE of the multiple regression model was approximately 4.7% lower on average than that of the IDW from April to August when the solar radiation was relatively high. However, it was discovered that the IDW was more accurate from September to January when the solar radiation was low as the MAPE obtained by the IDW was approximately 15.7% lower on average compared to the multiple regression model.
As shown in Fig. 5., the relationship of the prediction error MAPE according to the observed solar radiation was investigated to identify the tendency and cause of the IDW being inaccurate in a specific period. Compared to the prediction results of the multiple regression, the prediction accuracy of the IDW interpolation was 10.0% in the range of less than 4,000 Wh/m2·day, showing that it is approximately 2.4 times more accurate than the accuracy of the multiple regression model (24.2%). However, the multiple regression model exhibited better accuracy in the range above 4,000Wh/m2·day of solar radiation with an average MAPE of 7.3% compared to 12.2% of the average MAPE estimated by the IDW interpolation. In particular, in the range above 4,000Wh/m2·day of solar radiation, the IDW interpolation was found to be clustered according to the MAPE size of each case.
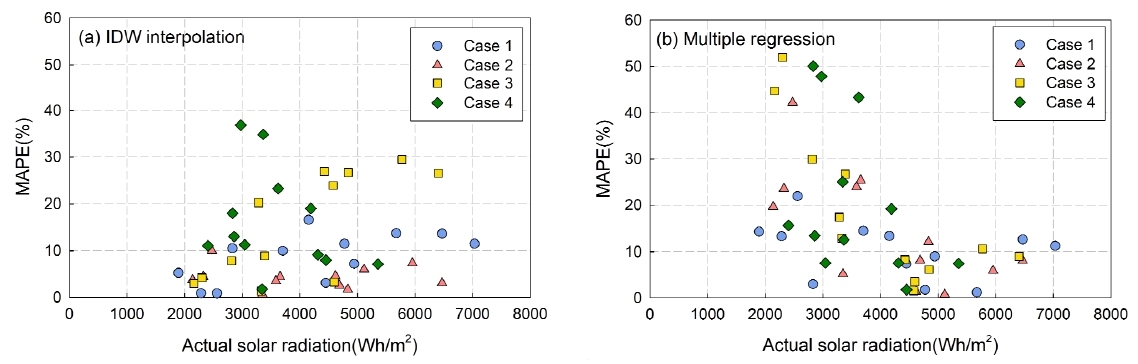
Accuracy of prediction by (a) IDW interpolation and (b )Multiple regression according to solar radiation
There may be complex factors behind the varying accuracy using the prediction method; however, it was determined when the distance between the point of case study and the nearest observation point used in the IDW interpolation is smaller, the MAPE in the range of large solar radiation was higher. More specifically, the distance of the nearest observatory for each case and the average MAPE from April to August were approximately 11 km and 25.6% for Case 3, 41km and 18.7% for Case 4, 45km and 12.3% for Case 1, and 58km and 4.6% for Case 2, respectively. If the nearest observatory is too close, the distance effect was excessively exerted, which resulted in low accuracy during periods with large solar radiation. Furthermore, since the regional scale of solar radiation is relatively small during the period of low solar radiation, the prediction errors were found to be small even when the distance effect was large.
5. Conclusion
In this study, the IDW interpolation method was used to predict solar radiation and evaluate the accuracy to improve the uncertainty in the prediction accuracy caused by the large distance between weather stations and predict the data of a randomly selected area in using the public data of the KMA.
A cross nation contour map of daily accumulated solar radiation was developed for each month by using the IDW interpolation method, and four observatories were selected as study cases and the corresponding prediction accuracies were evaluated.
Consequently, although the prediction accuracy varied by case, the average MAPE of the four cases was found to be approximately 11.06%, roughly 1.46 times more accurate than the MAPE estimated using the multiple regression model, which was 16.12%.
However, when the accuracy of the prediction models was identified for each month, the multiple regression model was found to be more accurate approximately 1.7 times compared to the IDW interpolation from April to August when solar radiation was relatively high and in the range of solar radiation above 4,000Wh/m2·day. The IDW interpolation was confirmed to be about 2.4 times more accurate with the MAPE of 10.0% compared to the multiple regression model from January to March and September to December when solar radiation was relatively low.
The IDW interpolation technology evaluated in this study is expected to be used to evaluate the adequacy of the areas to install PV power plants by searching for the most suitable location, and use it to predict the solar power generation or in an economic analysis and feasibility study. In particular, since it is advantageous in predicting the target point even when there are no benchmark data for predictive model learning. Hence, it is expected to be useful when it is difficult to collect data.
However, further improvement in error rates that can be particularly high in the range of large solar radiation is necessary. Future studies should aim to reduce the error rate by adjusting the pixel size and distance coefficient, which are precision indicators of prediction technologies and for determining a suitable distance from the nearest observatory.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1F1A1073949).
Reference
-
이창성, 지평식, ELM을 이용한 일별 태양광발전량 예측모델 개발, 한국: 전기학회논문지, 제64권 제3호, 2015, pp.164-168.
C.S. Lee, P.S. Ji, Development of Daily PV Power Forecasting Models using ELM, Korea: The Transactions of the Korean Institute of Electrical Engineers, 64(3), 2015, pp.164-168. [ https://doi.org/10.5370/KIEEP.2015.64.3.164 ]
-
H. Sharadga, S. Hajimirza, and R.S. Balog, Time series forecasting of solar power generation for large-scale photovoltaic plants, Renewable Energy, 150, 2020, pp.797-807.
[https://doi.org/10.1016/j.renene.2019.12.131]
-
C.A. Gueymard, D.R. Myers, Validation and ranking methodologies for solar radiation models, United States: Modeling Solar Radiation at the Earth’s Surface: Recent Advances, 2008, pp.479-509.
[https://doi.org/10.1007/978-3-540-77455-6_20]
- W. Ye, Spatial Variation and Interpolation of Wind Speed Staistics and Its Implication in Design Wind Load, Canada: The University of Western Ontario Doctorate thesis, 2013, pp.9-28.
-
박종철, 김민규, PRISM, 역거리가중법, 공동크리깅으로 작성한 1km 공간해상도의 남한 강수 자료에서 강수 분포의 비교, 한국: 한국지리정보학회 논문집, 제16권 제3호, 2013, pp.147-163.
J.C. Park, M.K. Kim, Comparison of Precipitation Distributions in Precipitation Data Sets Representing 1km Spatial Resolution over South Korea Produced by PRISM, IDW, and Cokriging, Korea: Journal of the Korean Association of Geographic Information Studies, 16(3), 2013, pp.147-163. [ https://doi.org/10.11108/kagis.2013.16.3.147 ]
-
D. Shepard, A Two-Dimensional Interpolation Function for Irregularly-Spaced Data, United States: Proceedings of the 1968 23rd ACM National Conference, 1968, pp.517-524.
[https://doi.org/10.1145/800186.810616]
-
박소우, 김주욱, 송두삼, 표준기상데이터 작성 시 누락된 풍속 데이터의 보간 방법 제안, 한국: 한국태양에너지학회 논문집, 제37권 제6호, 2017, pp.79-91.
S.W. Park, J.W. Kim, D.S. Song, A Proposal of an Interpolation Method of Missing Wind Velocity Data in Writing a Typical Weather Data, Korea: Journal of the Korea Solar Energy Society, 37(6), 2017.12, pp.79-91. [ https://doi.org/10.7836/kses.2017.37.6.079 ]
-
박성현, 회귀분석(제 3판), 한국: 민영사, 2007.
S.H. Park, Regression Analysis, The Third Edition, Korea: Minyoungsa, 2007.