복합재질로 구성된 건축 구조체의 열전달 수치해석을 위한 ISI10211모델계산
ⓒCopyright Korea Institute of Ecological Architecture and Environment
Abstract
The architectural structures in the engineering field include more than one material, and the heat transfer through these multiple materials becomes complicated. More or less, the analytic solutions obtained by the hand calculation can provide the limited information of heat transfer phenomena. However, the engineers have generally been forced to obtain reliable results than those of the hand calculation. The numerical calculation such as a finite volume methods with the unstructured grid system is only the suitable means of the analysis for the complex and arbitrary domains that consists of multiple materials. In this study, a new numerical code is developed to provide temperature distributions in the multiple material domains, and the results of this code are compared with the validation cases in ISO10211.
Finite volume methods with an unstructured grid is employed. In terms of numerical methods, the heat transfer conduction coefficient is not defined on the surface of the cell between different material cells. The heat transfer coefficient is properly defined to accurately mimic the heat transfer through the surface. The boundary conditions of heat flux considering radiation or heat convection are also developed.
The comparison between numerical results and ISO 10211 cases. We are confirmed that the numerical method provides the proper temperature distributions, and the heat transfer equation and its boundary conditions are developed properly.
Keywords:
Multiple material, Architectural structure, Computational methods, ISO10211, Boundary conditions키워드:
복합재질, 건물 구조체, 전산해석, ISO10211, 경계조건1. 서론
1.1. 연구의 배경 및 목적
건물 외피의 열성능에 대한 전열 해석 방법은 건물의 단열 성능, 결로 방지 성능, 에너지 소비 성능 평가 등 다양하게 활용이 가능하다. 특히 국내에서는 ‘공동주택의 결로 방지 설계 기준’(국토교통부, 2013년 12월)에 의거하여 공동주택 계획 시 단열 설계에 따른 결로 방지 성능에 대한 해석적 평가가 요구되고 있다. 건물의 열성능에 관련된 열에너지 전달 현상은 포아송방정식(Poisson's equation)으로 표현되며 단순형상에 대해서는 해석해를 얻을 수 있다. 그러나 형상이 복잡한 경우 해석적인 방법은 해를 구하기 어렵기 때문에 수치적인 방법을 이용한다. 수치적 방법은 관심을 가진 영역을 여러 개의 작은 격자(cell)로 나누고 작은 제어체적(격자)에 대하여 지배방정식(governing equation)인 열전도 방정식(포아송방정식)을 적용한다. 격자를 저장하는 자료구조의 형식에 따라 비정렬 격자(unstructured grid)와 정렬격자(structured grid)방식으로 구분되며 서로 인접한 격자는 배열의 인덱스(일반적으로 i, j, k)를 이용하여 기하학적 정보와 해석정보에 직접 접근이 가능하다.1) 좌표축과 나란하지 않은 형상에 대해서는 물리적영역(physical domain)을 계산영역(computational domain)으로 맵핑(mapping)하여 방정식을 새롭게 구성하거나 격자생성이 가능한 여러 개의 작은 영역으로 나누고 각각을 정렬격자로 구성하는 다중블록(multi-block)방법을 이용하여 제한적으로 복잡한 형상을 가진 영역에 적용이 가능하다.2) 그러나 정렬격자는 계산 영역의 형상이 복잡해짐에 따라 격자생성이 어렵거나 불가능해지는 단점을 가지고 있다. 최근의 복잡한 건축구조물이 일반화 되면서 정렬격자에 의한 계산은 줄어들고 있다.
비정렬격자는 형상의 제한이 없으며 복잡한 형상도 사용자의 개입 없이 양질의 격자를 생성할 수 있다는 장점을 가지고 있어 대부분의 상용해석프로그램은 비정렬격자를 사용하고 있다.3) 비정렬격자를 이용한 유한체적법(finite volume method, FVM) 은 해를 저장하는 방식에 따라 셀중심법(cell-centerd method), 격자중심법(vertex-centered method)으로 나눌 수 있으며 셀 중심방법은 해를 저장하는 방법이 단순하며 검사체적에 대하여 보간 방법을 사용하지 않으며 보존법칙을 만족하는 특징을 가지고 있어 많이 사용된다.4) 그러나 제어체적이 임의의 형상을 가지고 있으므로 2차이상의 정밀도를 구현하는데 어려움이 있다.5)
창문을 통한 열전달, 건축물의 벽면이나 우각호과 같은 건축구조물을 통한 열전달 문제는 대부분 2개 이상의 복합재질로 구성된다. FVM방법을 이용한 열전달 해석에서 인접한 두 격자가 서로 공유하고 있는 면(surface)에서는 이러한 물성치가 정의 되지 않는다. 면에서의 물성값은 실제 물성치와 반드시 일치할 필요는 없으며 인접한 두 격자간의 열전달을 정확하게 모사할 수 있도록 적절히 정의하면 된다. 본 연구는 3차원 전열해석(three dimension thermal transfer simulation)을 통하여 건물 외피의 열성능을 해석할 수 있는 해석 프로그램을 개발하기 위하여, 이전 연구인 단일재료로 이루어진 전열해석6, 7)에 이어 복잡한 형상에 적용이 가능하도록 3차원 비정렬격자를 이용하여 복합재료로 이루어진 영역의 전열해석을 하기 위하여 이산화, 복합재료간의 경계조건을 다루기 위한 수치적방법, 대류와 복사와 같이 열저항 경계에 관한 연구를 수행하였으며 ISO102118)에 제시한 2차원과 3차원 모델에 대하여 본 연구에서 사용한 차분화방법과 경계조건을 적용하여 얻은 결과를 비교하였으며 기존 상용코드9)와 그 결과를 비교하여 코드의 정확성을 검증하였다.
2. 전산응용 전열해석 이론
2.1 수송방정식
일반화된 적분형의 Reynolds수송방정식(Reynolds transport equation)형태의 열전도 방정식은 다음과 같다.5,7)
| (1) |
식(1)은 왼쪽부터 첫 번째 항은 시간에 따라 변화하는 양인 비선형항(unsteady), 두 번째 항의 확산항(diffusion)이며, 오른쪽항은 생성항(source term)을 나타낸다. 식(1)에서 t, ρ, V, S, T, Cp는 각각 시간(sec), 밀도(kg/m3), 체적(m3), 면 벡터(m2), 온도(K), 비열(J/kg∙K)을 나타낸다. 본 연구는 비정렬격자를 사용하기 때문에 확산항과 격자의 표면에서의 종속변수 값에 대한 적절한 모델링하거나 근사화가 필요하다.
2.2 셀중심-비정렬격자 이산화
3차원 열전도에서 6면체 외 다면체와 같은 복잡한 형태의 격자를 사용할 수 있는 비정렬격자에 있어서 이산화는 좌표와 무관하게 이루어져야 한다. 식(1)의 확산항은 가우스 이론(Gauss theorem)을 이용하면 제어체적의 표면적분으로 변환할 수 있으며 다음과 같이 격자의 형상에 무관하게 이산화 할 수 있다.
| (2) |
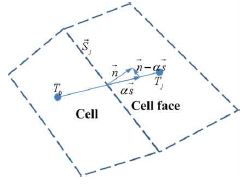
형상 격자의 중심에 종속변수(T)를 저장하며, 는 이웃한 미소제어체적(격자)과 공유하는 면(surface)의 면벡터를 나타내다. 이때 식(2)는 면에서의 적분을 나타냄으로 kj는 격자의 중심에서의 값이 아니라 격자의 표면 값을 나타낸다. k는 재료의 물성이므로 격자에 주어지며 표면에서는 주어지지 않는다. 그러므로 이 값은 격자의 면을 통해서 일어나는 열유속(heat flux) 정확하게 모사할 수 있도록 정하면 된다. 제어체적 표면 값인 을 구하기 위하여 Fig. 1에서와 같이 격자 중심을 연결하는 방향과 면벡터와 직각을 이루는 2개의 방향으로 나누고 에 대해서는 두 격자 중심점사이의 값으로 이산화하고 나머지 한 방향에 대해서는 적절히 모델링한다. 만약 가 제어체적의 표면과 나란하다면 두 벡터의 내적이 되어야함으로 이 된다. 이를 종합하면 다음과 같이 된다.
| (3) |
여기서 는 표면에 수직인 단위벡터를 나타내며, 는 방향의 단위벡터를 나타낸다.
식(3)에서 첫째 항은 두 격자의 중심방향을 따라 미분을 나타내며 유한 차분과 같은 방법으로 근사화 할 수 있다. 두 번째 항은 셀에서 얻은 값을 이용해서 벽면의 값으로 내삽 하여 사용할 수 있다.
| (4) |
| (5) |
α을 계산하여 대입하면 다음과 같이 된다.
| (6) |
| (7) |
만약 과 가 나란하다면 정렬격자와 같아지며 우변의 두 번째 항과 세 번째 항은 서로 상쇄되어 없어진다. 그러므로 FDM(finite Difference Method)의 중심차분한 값과 같아진다.
| (8) |
식(7)을 이용하여 확산항을 계산하면 다음과 같이 된다.
| (9) |
식(9)에서 오른쪽 두 항은 미지항으로 내재적(implicit)으로 다루며 나머지 항은 이전 반복의 값을 사용하여 생성항으로 처리하게 된다.10) 충분히 수렴한 해는 반복계산(iteration)에 무관하게 일정한 값을 가지게 됨으로 원래 방정식을 충족하는 해를 얻게 된다. 식(9)는 격자의 표면적분에 해당함으로 다면체격자의 경우 단지 면의 개수만큼 반복하면 된다.
2.3 복합재질 경계면처리
창이나 우각호, 건물의 벽체와 같이 관심영역이 여러 개의 서로 다른 물질로 구성되어 있는 경우, 격자의 경계면은 두 가지 물성이 다른 격자가 공유하게 됨으로 명시적으로 물성치가 정의 되지 않는다. 다만 인접하는 두 격자의 물성치를 이용하여 적절히 결정하여야 한다.
경계면에서의 값을 결정하는 가장 간단한 방법으로 인접한 격자의 열전도 계수를 평균하여 사용하는 방법이 있으며 다음과 같다.
| (10) |
여기서 ks는 경계면에서의 열전달 계수, k0 격자에서의 열전달 계수, kj인접격자에서의 열전달계수, w는 격자 중심 간의 거리와 격자 중심에서 경계면까지 거리비를 나타낸다. 만약 격자의 크기가 같다면 식(10)에서 w=0.5가 되어 산술평균이 된다. 산술평균은 수치적으로 간단하나 물리적으로 적절하지 않은 값을 유도하게 된다. 단적인 예로 만약 인접한 격자가 단열면이라면 kj→0이 되며 이면을 통한 열전달은 일어나지 않는다. 그러나 산술평균을 사용한 경우에는 단열이 아닌 재질의 1/2의 값을 가지게 됨으로 열전달이 이 면을 통해서 일어나는 불합리한 결과를 얻게 된다. 그러므로 복합재질의 경계면에서의 열전달 계수는 이면을 통한 열유속이 같아지도록 모델링 되어야 한다. 인접한 두 격자자간에 1차원적으로 가정하여 열전달에 해를 구하고 이를 이용하여 경계면에서 열전도 방정식을 구하면 다음과 같이 된다. 10)
| (11) |
식(11)은 경계면에서의 열전도 계수는 조화평균의 형태가 되어야 함을 나타낸다. 앞에서 보여준 예를 적용해 보면, 인접한 격자가 단열인 경우 ks=0이 되어 물리적으로 타당한 해를 얻을 수 있다. 본 연구에서는 식(11)의 식을 이용하여 경계면에서의 열전도계수를 구하였다.
2.4 경계조건
경계조건은 그 면에서 값이 주어지는 경계(Dirichlet boundary)와 미분 값이 주어지는 경계(Neumann boundary)로 나누어진다. 값이 주어지는 경우에는 추가적인 계산을 필요로 하지 않으며 주어진 값을 차분화 방정식에 넣고 명시적으로 처리하게 된다.1)
식(9)에서 인접한 격자 대신 경계의 온도를 사용하면 경계면에서 열전도는 다음과 같이 된다.
| (12) |
식(12)에서 오른쪽 항의 첫 번째 항과 세 번째 항은 주어진 값이 되며 명시적으로 처리하고 두 번째 항은 경계에 인접한 격자에서의 값으로 미지 값에 해당하며 암시적으로 처리하여 계수행렬에 더해 주게 된다. 또한 식(12)는 온도를 갖는 경계면에서 열유속을 구할 때 사용할 수 있다.
대류나 복사를 포함하는 경계에서는 수치대신 경계에서 미분값으로 열유속의 형태로 주어지게 된다. 이러한 경계는 경계면의 온도의 함수로 생각할 수 있으며 다음과 같이 선형화 모델링이 가능하다.
| (13) |
은 이전 반복계산(n-1)에서의 경계에서의 값으로 비선형 열유속를 이 값을 이용하여 선형화한다. 일반적으로 오른쪽 두 번째 항은 음(-)의 값을 가지며 경계에서 온도가 올라감에 따라 열유속이 감소하게 된다. 식 (12)와 (13)을 조합하면 다음과 같이 경계에서 온도를 배제한 방정식을 얻을 수 있다.
| (14) |
식(14)에서 오른쪽의 첫 번째 항은 내부 격자에서 온도이므로 암시적으로 처리하고 나머지 항은 명시적으로 처리한다. 경계에서의 온도도 식(14)와 비슷한 방법으로 구할 수 있다. 인접 격자에서의 온도가 구해지면 식(13) 혹은 식(14)을 이용하여 경계에서의 열유속을 구할 수 있다.
3. ISO10211모델 수치해석결과
3.1 ISO10211검증 모델설명
복합재질(multimaterial)로 구성된 창호나 벽체의 열전도 해석을 위한 수치코드를 검증하기 위해 ISO 10211부록의 대류, 단열, 온도경계를 포함하는 4가지 경우에 대하여 계산을 수행하고 그 결과를 비교, 검증하였다. 열전달 계산에 포함된 재질의 수와 경계조건에 관하여 Table 1에 나타내었다. CASE 1과 2는 2차원 문제이며, CASE와 3과 4는 3차원 문제이다.
FVM에 의한 열전도 방정식의 해석은 격자가 차지하는 영역에 대하여 그 중심의 값을 대표 온도로 나타내는 특성을 가진다. 격자가 많아짐에 따라 온도는 관심영역에 대해서 더욱 정밀하게 표현할 수 있다. 보존식을 사용함으로 적은 수의 격자로도 경계면에서의 열유속은 잘 만족하는 특성을 가지고 있다. 수치해석 코드는 정상상태(steady state)해석을 수행하였으며 최종적으로 얻어진 행렬식은 한 번의 수렴으로 바로 해를 얻을 수 있어 수렴히스토리는 제시하지 않았다.
본 연구에서 개발한 전열해석코드는 3차원으로 2차원의 경우 3차원 방향으로 임의의 높이를 가지는 1개의 격자만을 생성하고 3차원 방향의 경계는 적용하지 않는 방법을 사용하였다.
3.2 건축재료의 환경영향 정보 데이터베이스 구축
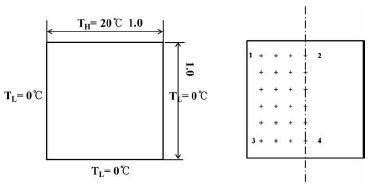
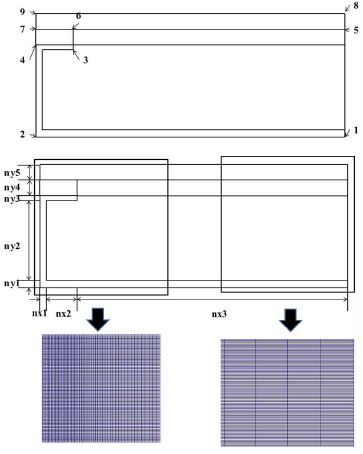
CASE01은 전형적인 2차원 문제로 온도경계로 둘러싸인 영역내의 열전도 문제이다. 상면을 제외한 모든 면은 0℃로 되어 있으며 상면은 20℃로 일정하게 유지된다. ISO10211에는 계산영역의 크기가 정확하게 나와 있지 않지만 이는 정상상태의 해로 한 변의 길이로 정규화(normalization)하면 상대적인 위치의 해는 모두 같기 때문이다. 본 연구에서는 계산을 간편하게 하기 위하여 한 변의 길이를 1로 하였다. 온도는 각 위치를 균등하게 나누어서 28곳을 ISO10211과 같이 측정하였으나 표시를 편리하게 하기 위하여 모서리의 값 4개만을 표시하였다. 격자의 개수를 바꾸어가며 계산을 수행하였으며 격자의 개수는 2배씩 증가시키며 수치해석을 수행하였다. 일반적으로 대칭임으로 계산영역을 반으로 나누어 계산을 수행하나 격자의 개수가 많지 않으므로 계산 영역을 반으로 나누지 않고 전체를 대상으로 수행하였다. 계산영역과 비교를 위한 온도점의 위치는 Fig. 2에 나타내었다.
본 연구에서 구현한 해석코드와 함께 상용소프트웨어인 STAR-CCM+을 이용하여 같은 형상에 대하여 계산을 수행하였다. STAR-CCM+격자는 육면체 격자를 사용하였으며 격자는 두 가지 다른 경우 8x4, 16x8의 격자를 사용하였다. 중간 면은 대칭면으로 반만을 계산 대상으로 하였다.
Table 2는 네 모서리에서의 온도 값을 ISO10211(이하 모든 표에서 ISO로 표기)에서 제시한 온도와 함께 표시하였으며 ISO10211에서 허용 오차는 모든 점에서 0.1℃를 넘지 않아야 한다고 제시하고 있다. 격자개수가 적은 경우 2번점에서 0.1℃보다 약간 넘어가는 것을 알 수 있다. 격자의 개수를 2배로 한 경우와 4배로 한 경우에는 허용 오차보다 작은 값을 나타내고 있다. 격자의 개수가 증가함에 따라 대체적으로 오차는 줄어드는 경향을 보이기는 하나 16x16보다 32x32가 반드시 작은 것은 아니다. 이는 해의 정확도를 나타내기 보다는 격자(cell)전체에 걸쳐 1개의 값이 대표 값으로 나타내기 때문에 발생하는 것이다. 온도는 취하는 점이 격자의 중심에 정확하게 일치하면 차이가 감소하고 그렇지 않은 경우 약간 늘어나게 된다. 모든 점을 나타내지는 않았으나 16x16과 32x32격자에서는 모든 점에서 허용오차보다 작은 값을 나타내었다. 16x16에서는 최대 오차가 0.071 이였으며 32x32에서는 0.042였다. 상용소프트웨어인 STAR-CCM+의 경우 Table 2에 추가적으로 표시하였으며 결과는 STAR-CCM+도 16x8의 격자를 사용하였으므로 본 연구의 16x16격자를 사용한 결과와 매우 흡사함 을 알 수 있다. 괄호 속은 ISO와 차이를 나타낸다.
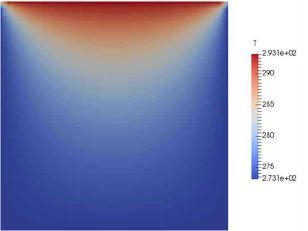
Fig. 3는 CASE01의 온도분포를 나타낸다. 전형적인 Laplace 방정식의 해를 보여주고 있다. 포물선의 형태로 중심부의 온도가 다른 부위에 비하여 크며 좌우대칭의 형태를 보여주고 있다. 계산영역내의 온도 분포는 경계에 의해 결정됨으로 293.15K에서 293.15K까지 나타나고 있다.
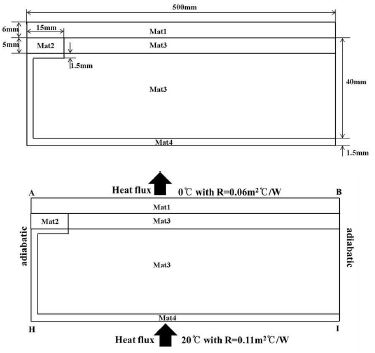
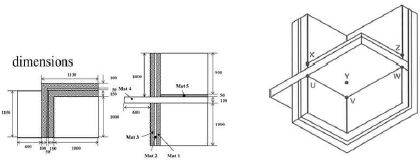
CASE02의 형상은 Fig. 4에 나타내었으며, 상부와 하부에서 참고온도(대류경계의 공기온도)는 0과 20℃이며 열저항을 각각 0.06, 0.11m·K/W을 가지고 있다. 이러한 경계는 일반적으로 벽면외부의 공기에 의한 대류를 가지는 경우라고 생각할 수 있으며 이 때 공기의 온도가 각각 0과 20℃ 가 되는 것으로 생각할 수 있다. 더운 공기에 접한 아래 면으로 열에너지가 들어와서 온도가 낮은 공기가 접한 상부로 빠져나가게 된다. 또 상부의 경계에 접한 면은 콘크리트로 되어 있으며 아래에 단열제가 있으며 아래면의 경계에 접해서는 알루미늄이 붙어 있다. 또 왼쪽의 상부에는 나무로 연결이 된 작은 부분이 있으며 이면은 알루미늄과 접해 있다.
CASE02는 형상도 비교적 복잡할 뿐 아니라 세로에 비하여 가로길이가 상당히 길어 균일한 크기의 격자보다는 상당히 큰 가로-세로비를 가진 비균일 격자(non-uniform grid)를 사용하였다. 각 영역의 물성치와 경계값을 Table 3에 나타내었다. Table 3에서 “AB”는 상부, “HI”는 하부의 고온부를 나타내며 Fig.4에 나와 있다.
Fig. 5는 CASE02의 격자와 비교를 위한 온도를 읽은 9개의 점들을 나타낸다. 비균일격자(non-uniform grid)을 사용하여 각 재료에서 열전달이 잘 모사되도록 하였으며 격자의 개수를 최소화 할 수 있도록 하였다. 계산영역의 크기가 상당히 길어 전체영역을 같은 길이로 사용하는 것은 매우 비효율적이며 온도를 적절히 예측하는데 어려움이 있었다. 본 연구의 격자는 Fig. 5에서 보듯이 양쪽 끝의 격자의 크기는 20배가 되도록 하였다. 이때 격자의 개수는 11664개의 격자를 사용하였다. 계산 영역이 길어 전체격자를 나타낼 수 없어 일부만을 표시하였다. 가로세로방향으로 몇 개의 구간을 나누고 각 구간의 격자의 개수를 조정해 가며 다양한 격자개수에 대해서 수행하였으며 그 중 몇 가지에 대한 결과를 나타내었다. 격자 개수를 조정하기 위한 변수는 Table 4에 나타내었다.
Mesh04에서 Mesh07로 갈수록 nx3의 격자수는 101에서 121로 증가시켰으며 비균일 격자의 비율을 4, 7, 12, 20으로 계속적으로 증가시켰다. 이 비율은 좌측면과 우측면 격자 크기의 비를 나타낸다. 즉 20인 경우는 왼쪽 격자의 가로 길이와 가장 오른쪽 격자의 가로 길이의 비는 20이 됨을 나타낸다. Fig. 5는 최종인 Mesh07의 격자를 나타낸다.
CASE02에 대하여 Fig. 5에 나타낸 9곳에서의 값들을 ISI10211에 제시된 값과 비교하였다. 격자 개수를 바꿈에 따라 내부 점(3, 4, 6, 7)의 값들이 조금씩 변하는 것을 관찰 할 수 있다. 이에 반해 경계에 접한 외부점은 거의 변하지 않는 것을 알 수 있다. 이것은 FVM의 특성으로 적분방정식을 사용하기 때문에 비교적 격자의 크기가 큰 경우에도 보존(conservation)이 만족되기 때문이다. 특히 열유속을 보게 되면 Mesh04와 같이 비교적 큰 크기의 격자를 사용함에도 불구하고 열유속를 잘 예측하고 있다. Mesh06과 Mesh07에서 내부점을 포함한 모든 점에서 허용오차를 만족한다. Table 5는 각 점에서 온도를 나타내며 Table 6은 ISO10211에서 제시한 온도와의 차이를 나타내고 있다. ISO10211에 제시한 값은 “ISO”로 표시하였다.
상용소프트웨어인 STAR-CCM+의 결과도 함께 나타내었다. STAR-CCM+에서 사용한 격자는 74600개의 다면체격자를 사용하였다. 온도분포는 본 연구의 코드에서 얻은 결과와 비슷한 정도를 나타내고 있다. 모든 점에서 온도와 열유속은 ISO10211에서 제시하는 허용오차를 만족하고 있다. STAR-CCM+의 결과는 본 연구의 Mesh06과 유사한 경향을 보이고 있다.
Fig. 6는 전체 영역에 대한 온도 분포를 보여주고 있으며 열전달이 잘 일어나는 알루미늄이 아래 부분 뿐 아니라 왼쪽 상단에서도 있어 다른 부분에 비하여 비교적 높은 온도를 나타내고 있다. 또 나무로 연결된 왼쪽 일부분은 알루미늄과 나무재질의 영향을 받으나 그 외의 영역에서는 길이 방향으로 온도 분포가 일정함을 알 수 있다. 즉 왼편의 알루미늄과 나무가 붙어있는 부분을 제외하고 대부분의 영역에서 1차원적인적도 온도 분포를 보여주고 있다.
CASE03은 단열벽과 벽체 사이에 열전도 매체(mat4)를 가지고 있다. 또 안과 밖의 경계는 열저항(대류조건)을 가지고 있으며 내측 상부와 외측의 온도차이는 15℃ 내측하부와 외측의 온도차는 20℃로 되어 있다. CASE02에서 설명한 것과 같이 열저항은 공기에 의한 대류조건으로 생각할 수 있으며 공기의 온도가 내측과 외측사이에 20℃차이가 난다. 또 상부와 하부 사이에는 추가적인 층이 있어 열전달은 벽체뿐 아니라 상부와 하부를 구분 짓는 mat4에 의해서도 일어난다. 열 저항을 가진 경계를 적절히 모델링하고 있는가와 각 재질간의 벽면을 통한 열유속의 모델링이 해의 정확성을 좌우하게 된다. 각 부위별 치수는 Fig. 7에 나타내었으며 열전달 계수는 Table 7에 나타내었다.
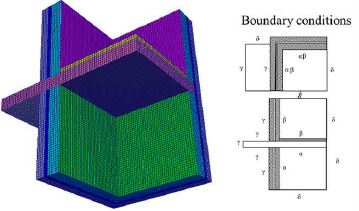
Fig 8는 CASE03 계산에 사용한 격자를 나타내었다. 격자는 전체 영역에 걸쳐 비슷한 크기의 육면체 격자를 사용하였으며 전체격자의 개수는 114368개이다. CASE03의 경계의 위치와 각 경계에서 열저항과 참고온도는 Table 8에 나타내었다.
Table 9에 각 면(α, β, γ, δ)을 통한 열유속을 나타내고 있으며 계산에 의해 얻은 전체 열유속은 59.792W/m2로 ISO10211보다 약간 작은 값을 보이고 있다. 상대오차는 0.33%로 ISO10211에서 제시한 허용 오차 1%보다 작은 값을 보이고 있다. α와 β도 비슷한 경향을 보이고 있다. 또 STAR-CCM+은 대부분의 영역에서 육면체를 가지며 경계면에서 일부 다면체 격자(trimmed mesh)를 사용하였다. STAR-CCM+의 경우 모든 면에서 본 연구의 열유속보다 약간 작은 값을 예측하였으나 ISO10211에서 제시한 1%보다는 작은 값을 보였다. 본 연구에서 사용한 수치적 모델링과 복합재질간의 경계면에서의 열전도계수, 경계조건은 적절히 모델링 된 것을 확인할 수 있다.
Fig. 9은 벽체의 온도분포를 보면 단열면을 지나면서 온도가 급격히 떨어지는 것을 알 수 있다. 또 상부와 하부를 가르는 mat4를 보면 온도 열전도도가 높으므로 내부에서는 높은 온도는 외부에 접한 면에서는 낮은 온도를 보이고 있다. 단열벽보다 넓은 면에서 온도의 변화를 관측할 수 있다. 전체에 비하여 작은 면이지만 mat4를 통해 열전도가 많이 일어나는 것을 확인할 수 있다. 상부와 하부면 또한 온도차가 나기 때문에 내측의 하부에서 상부로 열전도가 발생하고 있다. 상부에 비하여 하부에서 2배 이상의 열전달이 발생하고 있음을 알 수 있다.
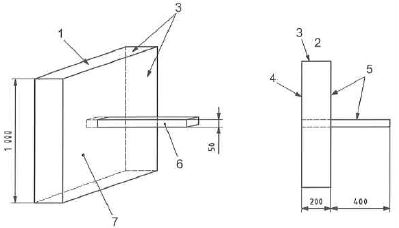
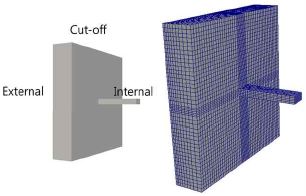
CASE04는 벽체에 금속의 막대가 관통을 하고 있으며 많은 열이 금속을 통해 전달되게 된다. Fig. 10에 전체적인 형상과 치수를 나타내었다. 벽은 단열벽에 해당하며 금속은 철에 해당한다. 각 부위별 물성치는 Table 10에 나타내었다.
경계는 단열과 열저항이 있는 내측과 외측으로 구성이 된다. 내외측의 온도변화는 1℃차이가 나며 각각 열저항은 0.1로 동일하다. 계산을 위한 격자는 형상을 고려해서 금속면에 접한 부분을 다른 면에 비하여 격자의 개수를 많이 넣었으며 벽체는 외부의 온도를 정확하게 표현하기 위하여 내측보다 외측에서는 격자의 크기가 작고 내측으로 들어올수록 크게 하였다. Fig. 11은 사용한 격자와 경계면들을 보여주고 있다. "Cut-off'는 절단면으로 Table 11에서 보면 단열면으로 되어 있다. 또 "Internal" 은 내부면으로 금속면들을 포함한다.
ISO의 결과에서 제시한 것은 전체면을 통한 열전달율과 외측면에서의 최고 온도 값을 제시하였다. ISO10211에서 열유속은 1%이내, 최고 온도는 0.005℃이하의 오차가 나야 한다고 제시하고 있다. 계산 결과를 Table 12에 나타내었으며 열유속은 0.536848W/m2로 오차율은 0.58%이며 외측면에서의 온도는 0.809℃로 ISO10211에서 제시한 값과 0.004℃의 차이를 보이고 있다. 두 값 모두 ISO10211에서 제시한 값보다 작으며 수치적 모델링이 열전달을 적절히 모사하고 있음을 알 수 있다. 중심의 금속부분을 제외하고는 대부분의 영역에서 1차원 적인 형태를 보이고 있다. FVM차분화의 특성상 적은 수로도 보존을 만족하게 됨으로 열유속과 온도를 적절히 예측하고 있다. STAR-CCM+ 은 Tmax는 본 연구에서 얻은 값과 같은 갓을 얻었으며 열유속은 0.37%의 오차로 본 연구에서 보다 다소 작은 오차를 보이고 있다.
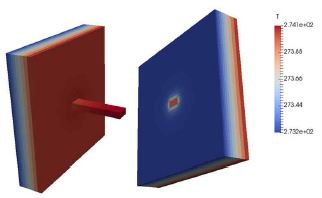
Fig. 12은 각 부위별 온도 분포를 보여주고 있다. 금속막대가 단열벽을 관통하고 있으므로 외벽의 중심에서 높은 온도 분포가 나타내고 있다. 모든 면이 절단면으로 단열로 되어 있으므로 온도분포는 1차원적인 형태를 나타내게 된다.
4. 결론
건물 외피의 열성능을 해석할 수 있는 해석 3차원 전열해석 프로그램을 개발하고 있으며, 해의 정밀도를 검증하기 위하여 ISO 10211에서 제시하는 검증 방법에 의거하여 2차원 3차원형상의 복합재질로 구성된 4가지 모델에 대한 해석을 실시하고 그 결과를 ISO에 제시한 값들과 비교하여 검증하였다. 또한 상용소프트웨어인 STAR-CCM+의 결과와 비교하였다. 본 연구에서 개발한 프로그램과 STAR-CCM+의 결과 모두 ISO10211에서 제시한 허용오차 내에 있었으며 CASE01, 02, 03에 대해서는 본 연구의 결과가 ISO10211와 근소하게 더 잘 일치하는 것을 확인하였다.
복합재질의 열전달 해석을 해석하기 위하여 서로 다른 물성치를 갖는 격자가 공유하는 면에서 열전달 계수를 열유속이 적절히 계산 될 수 있도록 모델링하였으며 또 경계면은 온도와 열저항을 갖는 다양한 경계조건을 다룰 수 있도록 하였다. 수치해석 결과는 계산을 수행한 4 경우 모두 ISO10211에서 제시한 정밀계산의 기준(CASE01에 관하여서는 0.1℃오차, CASE02에 관해서는 0.1℃오차, CASE03에 관해서는 1%오차, CASE04에 관해서는 1%, 0.005℃)을 만족하였다. 본 연구에서 개발한 열전달 해석 코드는 수치적 복합재질을 다룰 수 있도록 적절히 모델링되었음을 확인할 수 있었다. 본 연구에서 사용한 적분방정식의 FVM은 계산 영역에 걸쳐 보존을 만족시키며 비교적 적은 개수의 격자로도 열유속을 잘 예측함을 알 수 있었다. 향후 본 연구의 복합재질경계 계산을 바탕으로 창틀과 같이 복잡한 형상을 가진 3차원 형상에 대하여 자동적으로 전열해석을 수행하고 결로 생성위치 등을 예측할 수 있는 연구를 수행할 예정이다.
Acknowledgments
This research was supported by a grant(16RERP- B082204-03) from Residential Environment Research Program funded by Ministry of Land, Infrastructure and Transport of Korean government.
References
- Ferziger, Joel, Peric, Milovan, Computational Mechods for Fluid Dynamics, Springer-Verlag Berlin HJeidelberg, (1999).
- THOMPSON, Joe, F., WARSI, Zahir, UA, MASTIN, C. Wayne, Numerical grid generation foundations and applications, Amsterdam North-holland, (1985).
- H. K. MYONG, “Evaluation of Numerical Approximations of Convection Flux in Unstructured Cell-Centered Method”, Journal of computational fluids engineering, p36-42, (2006, Jan).
-
명현국, “비정렬 셀 중심 방법에서 대류플럭스의 수치근사방법 평가”, 한국전산유체공학회지, 11(1), p36-42, (2006).
H.K. Myong, Evaluation of Numerical Approximations of Convection flux in Unstructured Cell-centered method, Journal of kscfe, 11(1), (2006), p36-42. -
명현국, “비정렬 셀 중심 방법에서 확산플럭스의 새로운 수치근사방법”, 한국전산유체공학회지, 11(1), p8-15, (2006).
H.K. Myong, A New Numerical Approximation of Diffusion Flux in Unstructured Cell-Centered Method, Journal of kscfe, 11(1), (2006, Mar), p8-15. -
이주희, 장진우, 이용준, 최준혁, 이상환, “3차원 비정렬격자를 이용한 전열해석 방법론”, 대한건축친환경설비학회 논문집, 8(6), (2014).
Lee, Juhee, Jang, Jinwoo, Lee, YoungJun, Choi, Junhyuck, Lee, Sanghwan, Methodology for numerical heat transfer considering 3-dimensional unstructured grid, Journal of KIAEBS, 8(6), December), (2014, p343-348. -
이주희, 장진우, 이현균, 이용준, 이규성, “건물의 3차원 구조체에 대한 전열해석 프로그램 개발 중 서로 다른 열전도율을 갖는 복합재질 3차원 구조의 비정렬 격자에 대한 전산해석 방법”, 한국생태건축학회 논문집, 16(1).
Lee, Juhee, Jang, Jinwoo, Lee, Hyeonkyun, Lee, Youngjun, Lee, Kyusung, numerical heat transfer analysis methodology for multiple materials with different heat transfer coefficient in unstructured grid for development of heat transfer analysis program for 3 dimensional structure of building", KIEAE Journal, 16(1), (2016). [https://doi.org/10.12813/kieae.2016.16.1.081]
- ISO10211, Thermal bridges in building construction - heat flows and surface temperatures - Detailed calculations, First Edition, (2007, Dec, 15).
- STAR-CCM+ v402 Methodology, Computational dynamics Co., London, (2006).
- 명현국, CFD입문, 문운당, (2006).