난방시스템 최적 셋백온도 적용시점 예측을 위한 인공신경망모델 개발
**Samsung C&T Corporation, Construction Technology Center, Seoul, South Korea younju.yoon@samsung.com
***Corresponding Author, School of Architecture and Building Science, Chung-Ang University, Seoul, South Korea gilerbert73@cau.ac.kr
© Copyright Korea Institute of Ecological Architecture and Environment
Abstract
This study aimed at developing an artificial neural network (ANN) model to predict the optimal start moment of the setback temperature during the normal occupied period of a building.
For achieving this objective, three major steps were conducted: the development of an initial ANN model, optimization of the initial model, and performance tests of the optimized model. The development and performance testing of the ANN model were conducted through numerical simulation methods using transient systems simulation (TRNSYS) and matrix laboratory (MATLAB) software.
The results analysis in the development and test processes revealed that the indoor temperature, outdoor temperature, and temperature difference from the setback temperature presented strong relationship with the optimal start moment of the setback temperature; thus, these variables were used as input neurons in the ANN model. The optimal values for the number of hidden layers, number of hidden neurons, learning rate, and moment were found to be 4, 9, 0.6, and 0.9, respectively, and these values were applied to the optimized ANN model. The optimized model proved its prediction accuracy with the very storing statistical correlation between the predicted values from the ANN model and the simulated values in the TRNSYS model. Thus, the optimized model showed its potential to be applied in the control algorithm.
Keywords:
Artificial Neural Network, Predictive Controls, Heating Systems, Setback Temperature키워드:
인공신경망, 예측제어, 난방시스템, 셋백온도1. 서론
쾌적한 건물 실내 열 환경 조성을 위하여 작동되는 냉난방 시스템은 건물 에너지 소비의 중요한 요소 중의 하나이다. 주거건물의 경우 연간 사용되는 에너지의 양 중 약 58.1%를 냉난방 부분에서 소비하고 있는 것으로 조사되고 있다.1) 따라서 냉난방 에너지 소비를 감소시키기 위한 다양한 노력이 진행 중이며, 이들 중 시스템의 적절한 제어를 통한 건물 에너지 성능 향상이 시도되고 있다.
비재실기간(unoccupied period)동안의 시스템 작동을 위한 셋백(setback)온도의 적용은 불필요한 냉난방 에너지 소비를 방지하기 위한 효과적인 방법이다. 각종 실험, 시뮬레이션 및 현장측정 등을 적용한 선행연구들에 따르면 적절한 셋백 온도의 적용 시 23%의 냉방에너지 혹은 53%의 난방에너지의 절약이 가능한 것으로 조사되었다.1-8) 특히, 적절한 주/야간 셋백이 적용될 경우 한랭지역의 난방에너지 28.2% 및 냉방에너지 9.5%, 고온다습한 지역의 난방에너지 53.0%와 냉방에너지 16.9%를 절약할 수 있는 것으로 분석되었다.1)
셋백온도의 적용은 쾌적한 열 환경 제공이라는 기본적 목적을 고려하여 신중히 고려될 필요가 있다. 셋백기간의 시작 및 종료는 재실기간(occupied period) 동안의 쾌적한 열 환경 조성과 직접적 관련을 가지고 있다. 따라서, 적절한 셋백온도의 적용시점은 실내의 쾌적한 열 환경 및 건물 에너지 성능을 함께 고려하여 결정되어야 한다.
이러한 배경을 바탕으로 본 연구의 목적은 난방시스템의 최적 셋백 시작 시점을 도출하기 위한 인공신경망(Artificial Neural Network) 모델을 개발하는 것이다. 최적의 셋백 시작 시점이 적용될 경우 재실기간 중 불필요한 난방에너지 소비를 감소시킴과 동시에 비재실기간 중의 실내온도를 설정된 셋백 작동 범위에 보다 근접하게 유지시킬 수 있을 것으로 기대된다.
이러한 연구 목적을 달성하기 위하여 <그림 1>에 정리된 세 단계의 과정을 수행하였다. 첫 번째는 초기 인공신경망 모델을 개발(Initial Model Development)하는 단계이다. 이 단계에서는 초기 구조 및 학습방법이 설정되었다. 특히, 신경망모델의 입력변수와 출력변수 간의 상관관계분석(Correlational Relationship Analysis)을 통하여 유의미한 입력변수를 선정하여 모델에 적용하였다.
두 번째는 초기모델을 최적화(Model Optimization)하는 단계이다. 이 단계에서는 예측성능의 향상을 위하여 최적의 숨겨진층 수(Number of Hidden Layer, NHL), 숨겨진 층의 뉴런 수(Number of Hidden Neuron, NHN), 학습계수(Learning Rate, LR), 모멘텀계수(Moment, MO)를 도출하여 적용하였다. 최적화된 모델은 세 번째 단계인 성능테스트(Accuracy Test)를 통하여 예측의 정확도를 확인하였다.
모델개발, 최적화 및 성능테스트를 위하여 각각 학습데이터세트(training datasets), 최적화데이터세트(optimization datasets)와 체크데이터세트(check datasets)가 필요하다. 필요한 데이터 세트의 획들을 위하여 가상으로 구성된 모듈이 모델링되었다. 이에 대한 자세한 설명은 2 장에 설명되어 있다.
2. 인공신경망모델 개발
2.1. 초기모델 개발
본 연구에서의 예측 모델은 현재 실내온도에서 셋백온도까지 변화하기 위하여 필요한 시간(TIMESBT)을 예측하도록 계획되었다. 예를 들어 현재 실내온도가 25.0°C이고 셋백온도가 16.5°C일 경우 현재온도에서 셋백온도까지 변화하기 위해선 일정시간이 필요하게 되며, 개발된 모델은 이러한 필요 시간을 예측한다. 산출된 시간은 예측제어 알고리즘에 적용되어 실제 셋백이 시작되기 전에 난방장치의 작동을 멈추게 하는 역할을 한다.
예측모델의 개발을 위하여 인공신경망(Artificial Neural Network, ANN) 이론이 적용되었다. 인공신경망은 인간의 신경네트워크와 의사결정 및 학습의 과정을 수학적모델로 구현한 것으로써 비선형시스템 혹은 불명확한 역학을 내포하는 시스템 등의 제어를 위하여 성공적으로 적용되고 있다.9,10)
인공신경망 모델은 두 가지의 주된 과정을 수행한다. 첫 번째 과정은 일련의 입력 변수로부터 목적된 출력변수를 계산하는 과정이다. 이를 위하여 입력층(Input Layer)의 입력뉴런(Input Neuron), 숨겨진층(Hidden Layer) 및 뉴런(Hidden Neuron), 출력층(Hidden Layer)의 출력뉴런(Output Neuron)과 각 뉴런들 간의 관계(Connectivity, Weight)와 전이함수(Transfer Function)가 사용된다.
두 번째 과정은 학습의 과정으로써 제공된 학습데이터를 이용하여 지속적 학습을 진행함으로써 도출된 출력값의 오류를 줄이는 것을 목적으로 한다. 학습을 통하여 뉴런간 관계를 조정하게 된다. 이러한 두 가지의 과정을 통하여 예측제어(Predictive Control)와 적응제어(Adaptive Control)가 가능하게 된다.
인공신경망에 근간한 제어가 기존의 회귀모델(Regression Model) 혹은 PID(Proportional-Integral-Derivative) 모델 등의 수학적 모델에 의한 제어보다 정확하고 안정적인 것으로 연구되고 있다.11-19) 특히, 인공신경망에 의한 건물 냉난방시스템의 제어는 온도, 습도, PMV (Predictive Mean Vote)등 열 환경 용소를 보다 쾌적하고 에너지 효율적으로 조절하는 것으로 분석되었다.14-19)
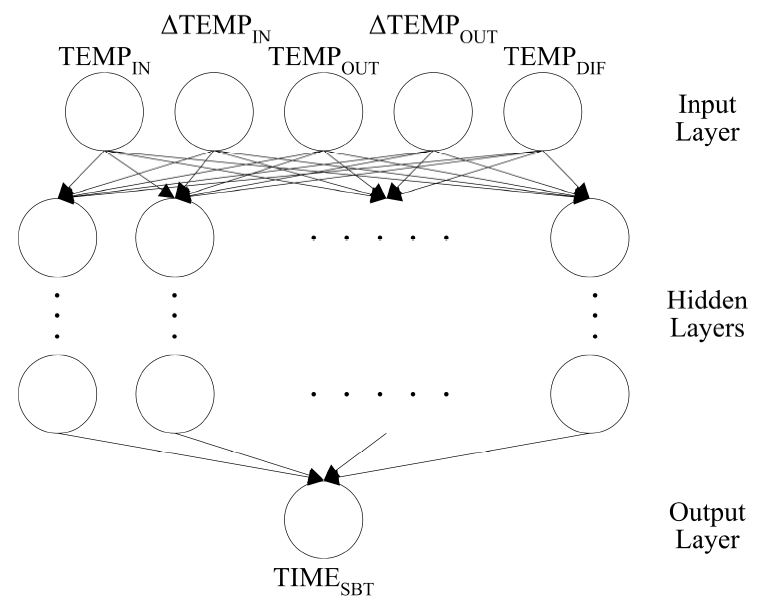
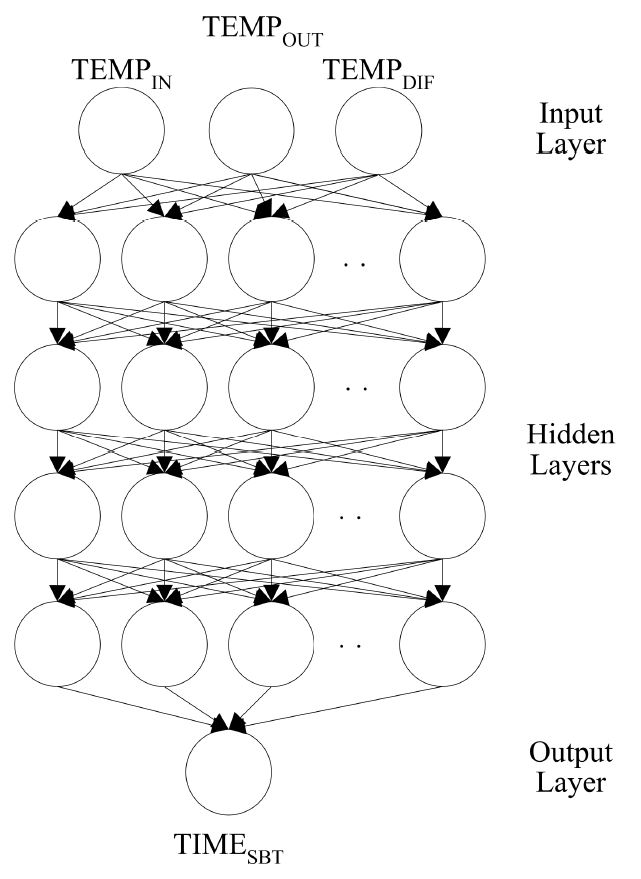
<그림 2>는 본 연구에서 개발된 초기 인공신경망 모델의 구조를 보여준다. 초기 모델은 기존연구의 결과를 바탕으로20,21) 현재실내온도(TEMPIN,°C), 지난 제어사이클로부터의 실내온도 변화(ΔTEMPIN,°C), 실외온도(TEMPOUT,°C), 한 시간 전부터의 실외온도 변화(ΔTEMPOUT,°C), 그리고 실내온도와 셋백온도와의 차이(TEMPDIF,°C) 등 다섯 가지의 입력뉴런을 가지도록 계획되었다. 각각의 뉴런은 10...30°C, -10...10°C, -20...40°C, -10...10°C, 그리고 0...10°C의 범위를 가지며 0~1의 값으로 치환되어 사용된다.
숨겨진층(NHL) 및 숨겨진층 뉴런의 수(NHN)는 기존 연구결과를20,21) 바탕으로 각각 3과 4로 설정되었다. 숨겨진 층의 뉴런을 위한 전이함수로는 Tangent-Sigmoid법이 적용되었다. 출력뉴런은 현재 실내오도로부터 셋백온도까지 변화를 위한 시간(TIMESBT, 분)으로 계획되었으며 pure-linear 변이함수가 사용되었다.
모델의 학습을 위하여 기존 연구 결과를20,21) 바탕으로 0.0-minute goal, 1,000-times epoch, 0.6-학습계수(Leargnin Rate, LR), 그리고 0.2-모멘텀계수(Moment, MO)가 적용되었다. 또한, <식 1>을 사용하여 81개의 학습데이터세트(Training Datasets)를 이용하여 학습을 진행하였다.
| Equation (1) |
초기모델의 계획 후 사용된 입력뉴런과 출력뉴런간의 상관관계분석(Correlational Relationship Analysis)을 실시하였다. 이를 통하여 출력뉴런과 관계가 깊은 입력변수를 도출하여 실제 입력뉴런으로 사용하였다. 이를 위하여 85개의 데이터세트에 대한 입력뉴런과 출력뉴런간의 R2가 계산되었다.
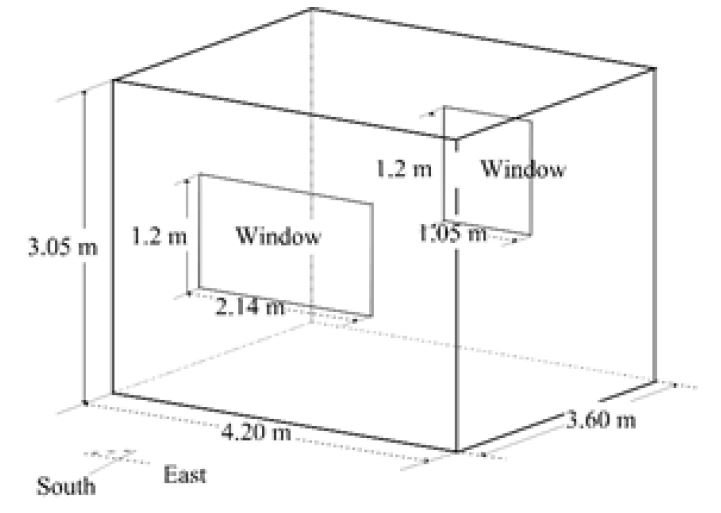
데이터세트는 겨울철(11월 1일~1월 31일)에 대하여 <그림 3>에 나타난 테스트모듈에서 획득되었다. 테스트모듈의 경계조건은 <표 1>에 정리되어 있다.
테스트모듈은 대한민국 서울에 위치하고 있는 것으로 가정하였으며, 대상지역에 대한 TMY(Typical Meteorological Year)2 기상데이터가 사용되었다. 대상지역의 겨울철 외기온도는 평균 1.7°C로 한랭하며, 여름철 평균기온 및 습도는 23.5°C와 72.7%로 고온다습한 기후이다.
모듈은 폭 4.2m, 깊이 3.6m, 높이 3.05 m의 크기를 가지며, 외피의 단열성능은 외벽 3.72, 지붕 6.80, 바닥 3.70, 창문 0.71 m2K/W로 적용되었다. 창면적비는 남쪽외벽 0.20 및 북쪽외벽 0.10으로 산정되었다. 실내부하는 2인의 재실자, 5 W/m2의 조명기기, 그리고 2대의 컴퓨터 및 프린터로 구성되었다. 1.5 ACH(Air Change per Hour)의 침기 및 환기가 있는 것으로 가정하였으며, 12,000 kJ/hr의 열 공급이 가능한 복사난방장치가 설치되었다.
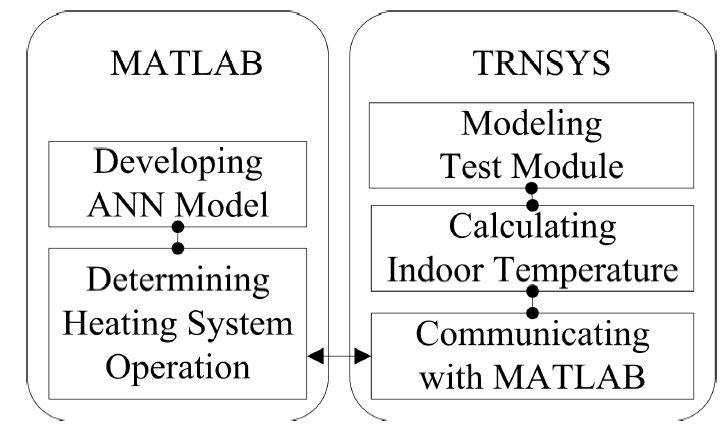
인공신경망 모델 개발, 테스트모듈의 모델링 및 데이터세트 획득을 위하여 Transient Systems Simulation (TRNSYS)23)와 Matrix Laboratory (MATLAB)24) 소프트웨어를 통합적으로 적용하였다. <그림 4>는 이러한 통합적 과정을 개념적으로 보여준다. MATLAB 소프트웨어는 인공신경망 모델의 개발과 난방 시스템의 작동을 결정하며, TRNSYS 소프트웨어는 테스트모듈의 모델링, 실내온도계산 및 MATLAB과의 연결을 위하여 사용되었다.
2.2. 모델 최적화
초기 인공신경망 모델은 보다 안정적이고 정확한 예측 결과의 도출을 위하여 구조와 학습방법의 최적화 과정이 수행되었다. 최적화 과정은 숨겨진층의 수(NHL), 숨겨진층의 뉴런 수(NHN), 학습계수(LR)와 모멘텀계수(MO)에 대하여 진행되었다. 최적화는 모델에서 예측된 TIMESBT와 시뮬레이션을 통하여 획득된 TIMESBT 간의 차이가 최소화되는 구조를 밝혀내어 적용함을 의미한다.
최적화된 수를 찾기 위하여 일련의 숨겨진층과 숨겨진층의 뉴런의 수가 동시에 적용되었으며, 이들에 대한 최적 개수를 도출한 후, 학습계수와 모멘텀계수가 동시에 분석되어 도출되었다. <표 2>에는 테스트되어진 매개변수의 값들이 정리되었다.
이러한 최적화과정을 위하여 100세트의 새로운 데이터세트가 위에서 설명한 테스트모듈에서 획득되었다. 각 데이터세트에 대하여 예측된 TIMESBT와 시뮬레이션된 TIMESBT의 상관관계분석(Correlational Relationship Analysis)을 실시하여 그 값이 최대가 되는 모델을 최적모델로 결정하였다.
최적화된 모델의 예측성능 분석을 위하여 또 다른 100세트의 새로운 데이터세트가 준비되었다. 새로운 데이터세트에 대한 예측된 TIMESBT와 시뮬레이션된 TIMESBT 간의 상관관계분석을 통하여 모델의 예측성능이 분석되었다.
3. 개발결과 및 성능분석
3.1. 초기모델 개발 결과
초기모델의 입력뉴런(TEMPIN, ΔTEMPIN, TEMPOUT, ΔTEMPOUT, TEMPDIF)과 출력뉴런(TIMESBT)과의 상관관계분석 결과가 <표 3>에 정리되어 있다. 상관관계는 셋백온도가 17.5°C에서 19.5°C 사이에서 변화하는 상황에 대하여 분석되었다.
TEMPIN, TEMPOUT, TEMPDIF 등 세 가지의 입력뉴런이 출력 뉴런과 상대적으로 높은 상관관계를 가지는 것으로 분석되었다. R2 값은 0.4556에서 0.9968의 범위에서 다양하게 나타났다. 반면, ΔTEMPIN과 ΔTEMPOUT은 출력변수와의 관계가 안정적이지 않은 것으로 분석되었다. 이러한 분석결과를 바탕으로 초기 인공신경망모델은 TEMPIN, TEMPOUT, TEMPDIF 세 가지를 입력뉴런으로 설정하였다.
특히, 상관관계는 셋백온도가 낮게 설정되었을 때 보다 강하게 나타났다. 즉, 정상설정온도와 셋백온도의 차이가 클수록 인공신경망모델은 TIMESBT를 정확히 예측하는 있을 것으로 예상할 수 있다.
3.2. 최적화 및 예측성능
초기모델의 최적화를 위한 첫 번째 단계는 NHL와 NHN의 최적 수를 예측된 결과값과 시뮬레이션된 결과값의 상관관계를 분석함으로써 진행되었다. 가장 큰 R2을 보이는 NHL과 NHN을 최적의 구조로 결정하였다.
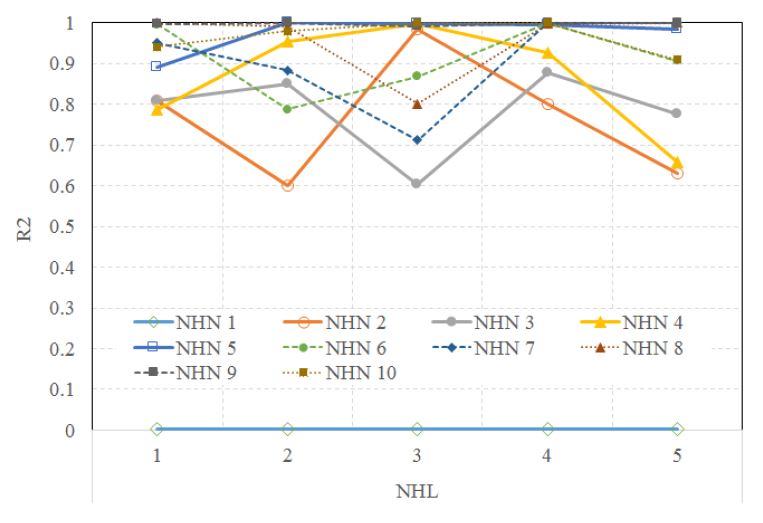
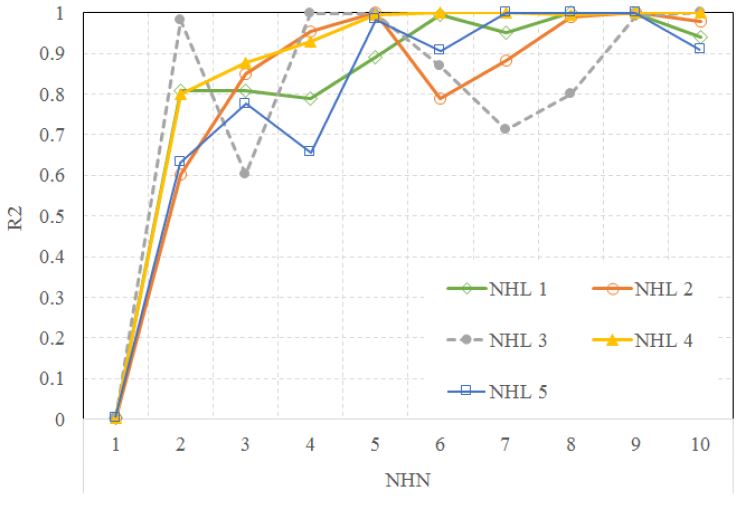
<그림 5>는 다양한 NHL 수에 대한 상관관계 분석 결과를 보여준다. 가장 높은 R2는 NHL의 수가 4개일 경우인 것으로 나타났다. 이 경우 R2는 0.8000(NHN이 2개일 경우)에서 0.9999(NHN이 9개인 경우) 사이에 분포하고 있는 것으로 분석되었다. NHN이 1개인 경우 예외적으로 낮은 0.0039 R2 결과값을 보이는데, 이는 숨겨진층 뉴런의 수가 1개일 경우 인공신경망 모델의 학습이 부적절히 이루어짐으로써 예측결과가 매우 부정확할 수 있다는 것을 의미한다. 이러한 현상은 모든 수의 NHL에서 공통적으로 발생하고 있다. 분석결과를 바탕으로 최적의 NHL 수는 4개로 결정되었다.
<그림 6>은 일련의 NHN에 대한 R2 분석결과를 보여준다. 가장 안정적인 상관관계는 NHN의 수가 9개일 경우인 것으로 분석되었다. 이 경우 R2는 0.9902(NHL이 3개인 경우)에서 0.9999(NHL이 4개인 경우) 사이이며, 그 평균값은 0.9979로써 상관관계가 매우 높은 것으로 나타났다. 따라서 최적의 NHN 수는 9개로 결정되었다.
최적화 두 번째 단계는 LR와 MO의 최적 수를 결정하는 것이다. 이전 단계와 동일하게 가장 큰 R2 값을 보이는 수를 최적의 구조로 결정하였다. 인공신경망모델은 이전 단계에서 밝혀진 최적의 NHL(4), NHN(9) 구조로 고정된 후 LR과 MO 값을 변화시키면서 분석이 진행되었다.
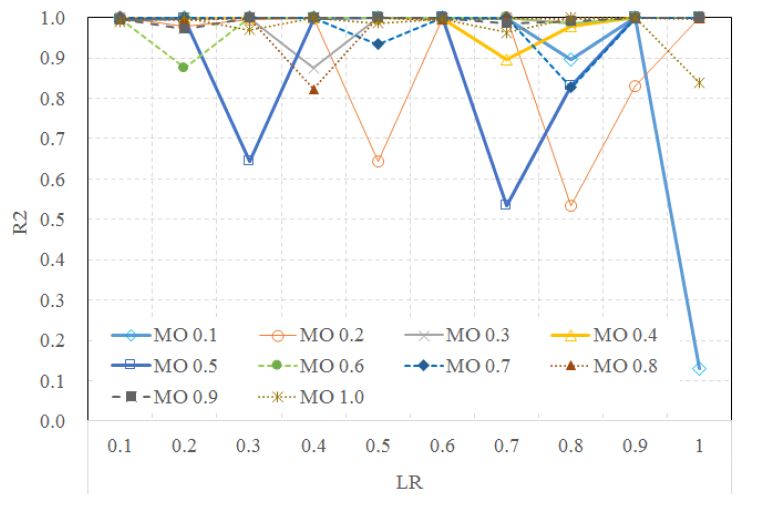
<그림 7>은 다양한 LR 값에 대한 상관관계 분석 결과를 보여준다. 가장 높은 R2는 LR의 값이 0.6일 경우인 것으로 나타났다. 이 경우 R2는 0.9942에서 0.9999 사이이며 평균 0.9981인 것으로 분석되었다.
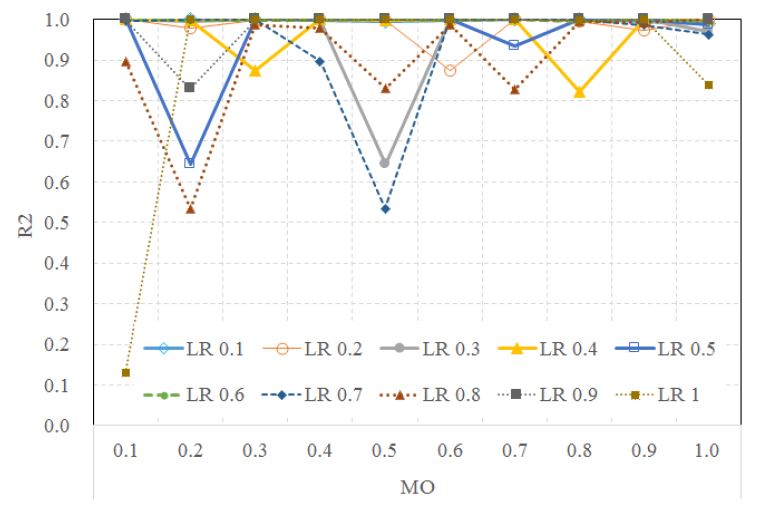
<그림 8>은 일련의 MO에 대한 R2 분석결과를 보여준다. 가장 안정적인 상관관계는 MO의 값이 0.9일 경우인 것으로 분석되었다. 이 경우 R2는 평균 0.9943에 이르는 것으로 나타났다. 분석결과 최적의 LR과 MO값은 각각 0.6과 0.9로 결정되었다.
<그림 9>는 최적모델의 구조를 보여준다. 최적모델은 출력뉴런 TIMESBT의 계산을 위하여 입력뉴런으로써 TEMPIN, TEMPOUT, TEMPDIF를 가지며, 4개의 NHL, 9개의 NHN, 0.6 LR, 0.9 MO의 구조를 가지게 되었다.
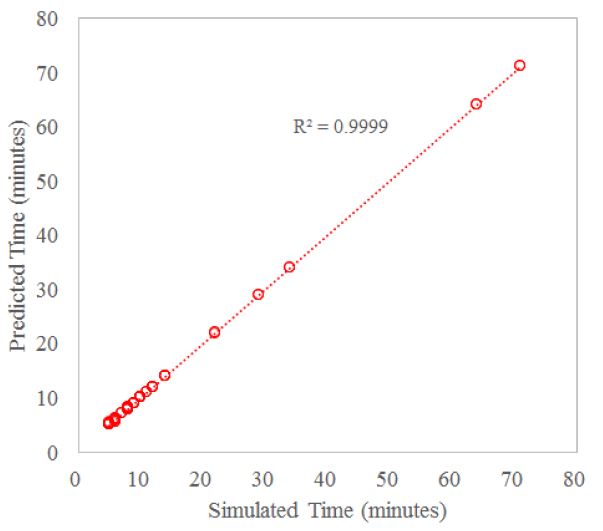
<그림 10>은 최적화된 모델의 예측성능을 분석하기 위하여 최적모델에서 계산된 TIMESBT와 시뮬레이션에서 계산된 TIMESBT의 결과를 비교한 것이다. 비교 결과 R2는 100 가지의 테스트 경우에 대하여 0.9999의 높은 상관관계를 보여주었다. 따라서, 개발된 모델의 적용성이 증명되었다.
4. 결론
본 연구는 최적의 셋백 시작 순간을 적용하기 위하여 현재 실내온도로부터 셋백 온도까지 변화하기 위한 시간을 예측하는 인공신경망 모델을 개발하는 것을 목적으로 하였다. 이를 위하여 초기 인공신경망 모델 개발, 모델 최적화, 성능테스트의 세 단계를 진행하였다. 각 개발 단계에서 밝혀진 결과는 다음과 같다.
(1) 입력뉴런과 출력뉴런간의 상관관계분석 결과 TEMPIN, TEMPOUT, TEMPDIF가 관련성이 높은 것으로 밝혀짐으로써 초기 모델은 이 세 가지 변수를 입력뉴런으로 가지게 되었다.
(2) 모델최적화를 위하여 일련의 NHL, NHN, LR, MO에 대한 예측 성능 분석이 실행되었으며, 그 결과 4개의 NHL, 9개의 NHN, 0.6 LR, 0.9 MO의 구조가 가장 정확한 예측을 하는 것으로 분석되었다. 따라서, 최적 모델은 이러한 값을 가지는 구조로 변경되었다.
(3) 최적화된 모델의 성능 분석을 위하여 100가지의 경우에 대한 예측결과를 시뮬레이션 결과와 비교하였다. 그 결과 0.9999 R2의 상관관계를 보임으로써 안정적이고 정확한 예측이 가능할 수 있는 것으로 분석되었다. 따라서, 개발된 인공신경망 모델은 추후 난방시스템의 제어를 위한 알고리즘에 적용되어 최적의 셋백 시작 시간에 근간한 효율적 열 환경제어에 일조할 것으로 기대된다.
본 연구는 모델의 성능분석을 위하여 가상의 테스트모듈에서 획득된 데이터를 사용하였다. 또한, 모델의 결과값은 난방시스템의 작동을 위한 결과물을 도출하도록 계획되었다. 따라서, 추후연구에서는 여름철 냉방시스템을 위한 모델의 개발과 더불어 제어 알고리즘의 개발이 진행되어야 할 것으로 판단된다. 또한, 실제 건물에서의 성능분석을 통하여 개발된 모델의 적용성을 확증할 필요성이 있는 것으로 사료된다.
Nomenclature
| TIMESBT : | predicted time required to reduce the current indoor temperature to the setback temperature, minutes |
| TEMPIN : | indoor air temperature, °C |
| ΔTEMPIN : | change from the indoor air temperature of the preceding control cycle, °C |
| TEMPOUT : | outdoor air temperature, °C |
| ΔTEMPOUT : | outdoor air temperature change from one hour ago, °C |
| TEMPDIF : | temperature difference from the setback temperature, °C |
| NHL : | number of hidden neurons |
| NHN : | number of hidden neurons |
| NIN : | number of input neurons |
| NON : | number of output neurons |
| ND : | number of training datasets |
| LR : | Learning Rate |
| MO : | Moment |
Acknowledgments
본 논문은 2016년도 서일대학교 학술연구비에 의해 연구되었음.
References
-
Moon, J.W., Han, S., Thermostat strategies impact on energy consumption in residential buildings, Energy and Buildings, 43, (2011).
[https://doi.org/10.1016/j.enbuild.2010.09.024]

- Manning, M.M., Swinton, M.C., Szadkowski, F, Gusdorf, J., Ruest, K., The effect of thermostat set-back and set-up on seasonal energy consumption, surface temperatures and recovery times at the CCHT Twin House Facility, ASHRAE Transactions, 113, (2007).
-
Ingersol, J.l., Huang, J., Heating energy use management in residential buildings by temperature control, Energy and Buildings, 8, (1985).
[https://doi.org/10.1016/0378-7788(85)90012-X]

- Beckey, Y., Nelson, L.W., Field test of energy savings with thermostat setback, ASHRAE Journal, 23, (1981).
- Nelson, L.W., Ward, M.A., Energy savings through thermostat setback, ASHRAE Journal, 9, (1978).
- Nelson, L.W., MacArthur, J.W., Energy Savings through Thermostat Set-back, ASHRAE Transactions, 83, (1977).
-
Rosenfeld, A.H., Notes on residential fuel use: Thermostat and window management, Energy and Buildings, 1, (1977).
[https://doi.org/10.1016/0378-7788(77)90020-2]

- Nelson, L.W., Reducing fuel consumption with night setback, ASHRAE Journal, 15, (1973).
- McCulloch, W., Pitts, W., A Logical Calculus of Ideas Immanent in Nervous Activity, The Bulletin of Mathematical Biophysics, 5, (1943).
- Moon, J.W., Kim, J.J., ANN-based thermal control methods for residential buildings, Building and Environment, 45, (2010).
- Kalogirou, S.A., Neocleous, C.C., Schizas, C.N., Building Heating Load Estimation Using Artificial Neural Networks, In: Proceedings of the International Conference “CLIMA 2000”, Brussels (Belgium), (2003).
- Shin, K.W., Lee, Y.S., The study on cooling load forecast of an unit building using neural networks, International Journal of Air-Conditioning and Refrigeration, 11, (2003).
-
Moon, J.W., Jung, S.K., Kim, Y., Han, S., Comparative study of artificial intelligence-based building thermal control methods – Application of fuzzy, adaptive neuro-fuzzy inference system, and artificial neural network, Applied Thermal Engineering, 31, (2011).
[https://doi.org/10.1016/j.applthermaleng.2011.04.006]

-
Moon, J.W., Performance of ANN-based predictive and adaptive thermal control methods for disturbances in and around residential buildings, Building and Environment, 48, (2011).
[https://doi.org/10.1016/j.buildenv.2011.06.005]

-
Morel, N., Bauer, M., El-Khoury, M., Krauss, J., NEUROBAT, a predictive and adaptive heating control system using artificial neural networks, International Journal of Solar Energy, 21, (2001).
[https://doi.org/10.1080/01425910108914370]

-
Ben-Nakhi, A.E., Mahmoud, M.A., Energy conservation in buildings through efficient A/C control using neural networks, Applied Energy, 73, (2002).
[https://doi.org/10.1016/S0306-2619(02)00027-2]

-
Argiriou, S.S., Bellas-Velidis, I., Kummert, M., Andre, P., A neural network controller for hydronic heating systems of solar buildings, Neural Networks, 17, (2004).
[https://doi.org/10.1016/j.neunet.2003.07.001]

-
Abbassi, A., Bahar, L., Application of neural network for the modeling and control of evaporative condenser cooling load, Applied Thermal Engineering, 25, (2005).
[https://doi.org/10.1016/j.applthermaleng.2005.04.006]

- Ruano, A.E., Crispim, E.M., Conceicao, E.Z.E., Lucio, M.M. Jr, Prediction of building’s temperature using neural networks models, Energy and Buildings, 38, (2006).
-
Yang, I., Kim, K., Prediction of the time of room air temperature descending for heating systems in buildings, Building and Environment, 39, (2004).
[https://doi.org/10.1016/j.buildenv.2003.08.003]

-
Moon, J.W., Kim, K., Min, H., ANN-Based Prediction and Optimization of Cooling System in Hotel Rooms, Energies, 8, (2015).
[https://doi.org/10.3390/en81010775]

-
Moon, J.W., Lee, J., Yoon, Y., Kim, S., Determining optimum control of double skin envelope for indoor thermal environment based on artificial neural network, Energy and Buildings, 69, (2014).
[https://doi.org/10.1016/j.enbuild.2013.10.016]

- University of Wisconsin, TRNSYS16.1, Available from: http://sel.me.wisc.edu/trnsys/. 2015-10.
- MathWorks, MATLAB 14, 26, Available from: http://www.mathworks.com. 2014-11.