창틀 공기층의 유효 열전도율(λeff) 산정방법 차이가 창 전체 열관류율(Uw) 시뮬레이션 결과에 미치는 영향에 대한 비교 분석 - 단창 창틀의 비환기 공기층에 대한 시뮬레이션을 중심으로
© Copyright Korea Institute of Ecological Architecture and Environment
Abstract
It is difficult to calculate frame U-value because of the two reason. First is selection of air properties in cavity . Second is calculation method in window frame. For this reason, it is important to decide cavity properties in window frame. However, international standards offered different method(ISO 15099, ISO 10077) and air properties was changed according to the two methods. The aim of this study was to suggest method for deriving accurate frame U-value using international standard methods and CFD simulation.
First, this study conducted analysis calculation method of ISO 15099 and ISO 10077. And, CFD simulation conducted based on same condition. Finally, ISO calculation and CFD simulation results were verified through comparison with real experiment results.
The results show that effective conductivity of ISO 15099 was the highest value. ISO 10077 and CFD result followed. The convergent values of ISO 10077 was the highest. ISO 15099 and CFD followed. ISO calculation reflecting CFD simulation results will reduce error with experimental results.
Keywords:
Fenestration energy consumption efficiency rating system, Total window thermal transmittance, Frame cavity effective conductivity키워드:
창세트 에너지소비효율등급제, 창세트 열관류율, 창틀 공기층 유효열전도율1. 서론
1.1. 연구의 배경 및 목적
국내 고성능 창호의 개발 및 보급 확대를 위하여 2012년 7월부터 산업통상자원부에서 ‘창세트 에너지소비효율등급 표시제도’가 시행되고 있으며, 이와 함께 제도의 활성화와 창세트 에너지소비 성능 평가의 효율화를 위하여 상기의 제도에 더하여 2013년 6월부터 시뮬레이션 방법을 이용하여 창세트의 열관류율을 평가할 수 있도록 개정되었다. 시뮬레이션 방법을 활용하여 창세트의 에너지소비효율등급 중 열관류율 성능을 평가하기 위해서는 실물 실험과 시뮬레이션 평가법의 결과가 상응하는 정확성을 확보하여야 한다. 현재 각국에서 적용하고 있는 창세트의 열관류율 평가 방법은 두 가지 국제 표준인 ISO 15099와 ISO 10077에 기반한 평가 방법을 주로 채택하고 있으며, 특히 국내에서도 ‘창세트 에너지소비효율등급 표시제도’를 위한 평가 방법으로 ISO 15099에 근거한 평가 방법을 시뮬레이션 평가법으로 활용하고 있다. 국제 표준에서 제시하는 시뮬레이션 평가 방법은 유리 구성, 간봉의 종류, 창틀의 설계에 따라 유리의 열관류율(Ug), 창틀의 열관류율(Uf), 유리와 창틀 경계인 edge부의 열관류율(Ue) 또는 해당 부위에 대한 선형 열관류율(Ψ)을 계산하고 창세트의 구성에 따른 각 부위별 면적 또는 적용 길이를 이용하여 전체 창세트의 열관류율(Uw)을 산출하도록 되어 있다. 이 중 창세트의 에너지성능에 영향을 미치는 창틀의 열관류율(Uf)을 산출하는데 있어서, 창틀 내 많은 부분을 차지하는 공기층(cavity)에 대한 해석 방법은 적용하는 국제 표준에 따라 다른 수식을 제공하고 있으며, 이에 따른 공기층의 물성도 차이가 있어, 창틀 열관류율(Uf)에 차이가 발생한다.
이에 본 연구에서는 국제 표준에서 제시하고 있는 창틀 내 공기층에 대한 물성 산출 방법과 함께 공기층에 대한 보다 정밀한 해석 방법인 전산유체역학(Computational Fluid Dynamics, CFD)을 이용하여 공기층의 열유동 해석에 의한 물성 도출 결과를 비교하여 보다 정확한 물성의 선정과 이를 통한 창틀 열관류율(Uf) 시뮬레이션 결과의 고도화를 위한 기초 자료를 제공하는 것을 목적으로 하였다.
1.2. 연구의 방법 및 범위
본 연구에서는 두 가지 국제 표준에서 제시하고 있는 공기층, 특히 ‘비환기 공기층’(Unventilated frame cavity)에 대한 물성 산정 수식을 중심으로 비교 대상 표준별 공기층의 물성 산출 결과를 비교하고, 또한 공기층의 열전달 시뮬레이션을 위한 정밀해석 방법인 CFD 해석을 통하여 동일한 조건에서의 열유동 해석을 통한 물성 도출 및 비교 분석을 실시하였다. 또, 각 국제 표준을 적용하여 개발된 평가 프로그램을 활용하여 실제 창세트에 대한 해석을 실시하여 평가법에 따른 해석 결과와 실물 실험 결과와의 상응도를 확인하였다.
본 연구에서 비교하고자 하는 국제표준(ISO Standard)은 ISO 15099와 ISO 10077로서 각 표준에서 산출법을 제시하고 있는 공기층의 물성은 공기층을 고체로 가정하고 시뮬레이션 할 수 있도록 공기층의 형상, 열류 방향 등에 따른 ‘유효 열전도율’(effective conductivity)을 산출하는 수식을 제공한다. 본 연구에서는 각 평가법에 대한 비교를 위하여 다양한 공기층 형상을 대안으로 설정하여 물성을 산출, 비교 분석을 실시하였다. 단, 본 연구에서는 단창 창세트(Single window)만을 대상으로 하였는데, 이는 국제 표준에서 제시하고 있는 평가법상에서는 국내의 일반적인 이중창(Double window)에 대한 계산이 가능한 이론적인 방법을 제시하지 않고 있기 때문이다. 즉, 국내에서 일반적으로 적용되고 있는 이중창의 실내외 측 창간의 이격거리가 약 70mm ~110mm의 범위로 형성되고 있는데, 국제 표준에서 제시하고 있는 평가법에서 계산을 통하여 평가 가능한 중간 공기층의 최대 간격은 50mm로 제한되어 있고, 그 이상의 공간이 형성되는 창세트의 경우, 보다 정밀한 해석 방법이나 실물 실험 결과를 활용하도록 규정하고 있다.
2. 유효 열전도율(λeff) 산출을 위한 이론식 비교
2.1. ISO 15099의 유효 열전도율 산정 수식
본 연구에서 비교하고자 하는 국제표준 중 ISO 15099에 제시된 유효 열전도율 산정 수식은 다음과 같다.
| [1] |
ISO 15099는 상기의 기본 수식에서 hcv를 산정 시 열류 방향과 형상에 따라 구분하여 수식을 제공하며, 이를 정리하면 다음과 같다.
(1) 하향 열류인 경우
| [2] |
(2) 상향 열류일 경우
- ① Lh/Lv ≦ 1, Nu = 1.0
- ② 1 < Lh/Lv ≦ 5
[3]
[4]
[5] - ③ 5 < Lh/Lv
[6]
(3) 수평 열류일 경우
- ① Lv/Lh < (1/2)
[7] - ② (1/2) < Lv/Lh ≦ 5
[8] - ③ 5 < Lv/Lh 인 경우에는 앞서 제시한 ①, ②형상에 따른 극값에 대하여 보간하여 구한다.
2.2. ISO 10077의 유효 열전도율 산정 수식
ISO 10077-2의 경우 다음의 식을 기본 식으로 하여 공기층의 폭에 따라 다음의 두 가지 경우로 구분하여 ha를 산출한다.
| [9] |
(1) b(공기층 폭) < 5mm일 경우
| [10] |
2) b(공기층 폭) ≧ 5mm일 경우
- ① △T를 아는 경우
[11]
C1 = 0.025 W/mK, C2 = 0.73 W/㎡K4/3 - ② △T를 모르는 경우
[12]
이때 공기층의 형상이 복잡한 경우 ISO 10077-1에서 제공하는 규칙에 따라 간략한 형상으로 가정하여 계산을 수행하였다.
3. 국제 표준에 따른 유효 열전도율(λeff) 비교
본 연구에서는 앞 절에서 제시한 수식을 모두 반영할 수 있는 공기층 형상 Case를 설정하여 각 Case별 유효 열전도율을 산출 비교하였다.
3.1. 공기층 형상 Case의 설정
본 연구에서 비교하고자 하는 국제 표준에서 제시하는 열류 방향별 공기층의 형상을 모두 반영하기 위해서, 공기층의 형상을 다음의 Table 1과 같이 7개의 Case로 구분하였다.
또한 각각의 형상 Case에 대하여 열류 방향에 따른 공기층 두께(d)를 변수로 하여 총 175 case에 대하여 각 표준에 따른 유효 열전도율을 산출 비교하였다.
3.2. Case별 산출 방법에 따른 유효 열전도율 비교
공기층의 형상에 따른 유효 열전도율 산출 결과를 정리하면 다음과 같다.
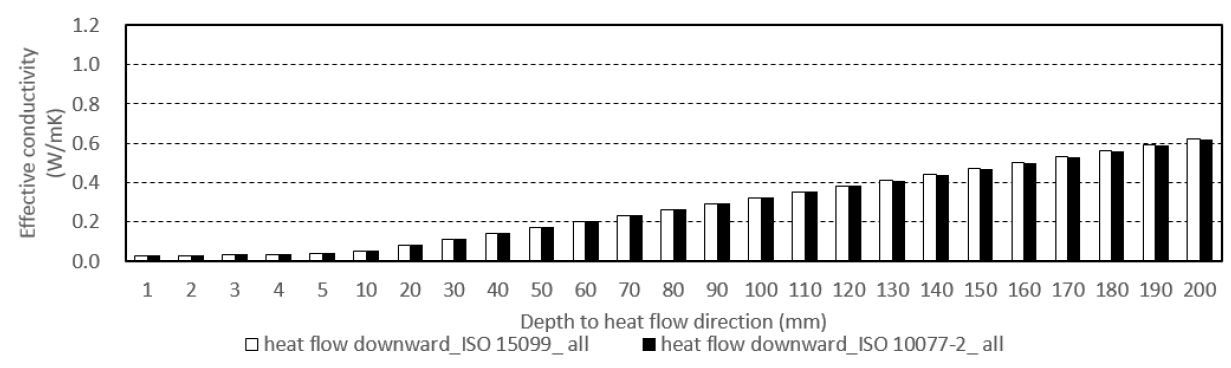
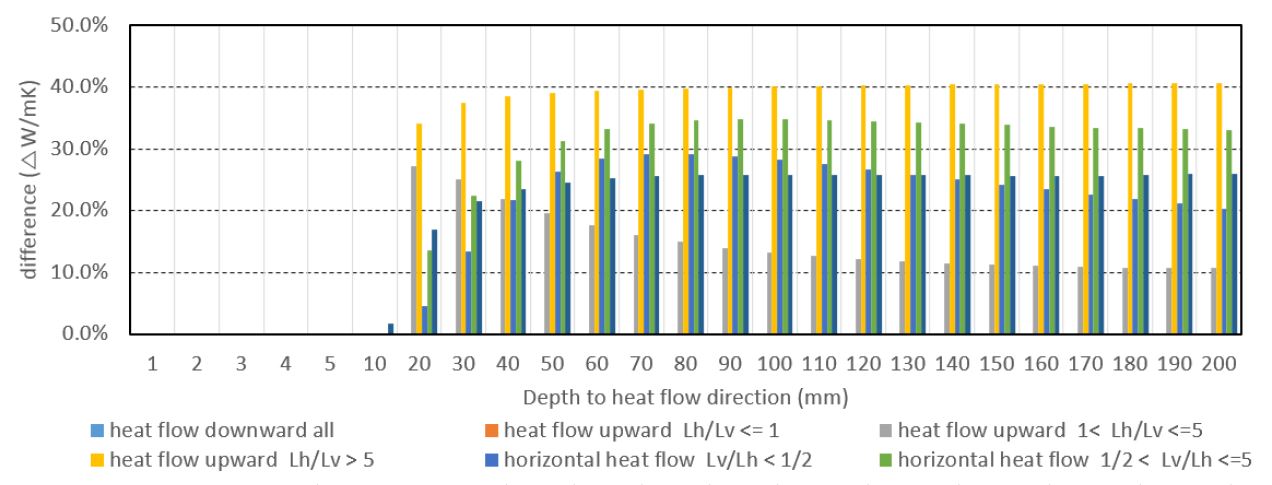
(1) 하향 열류 방향인 경우, 두 표준에 따른 유효 열전도율 산출 결과가 검토한 모든 범위에서 거의 동일하였다.
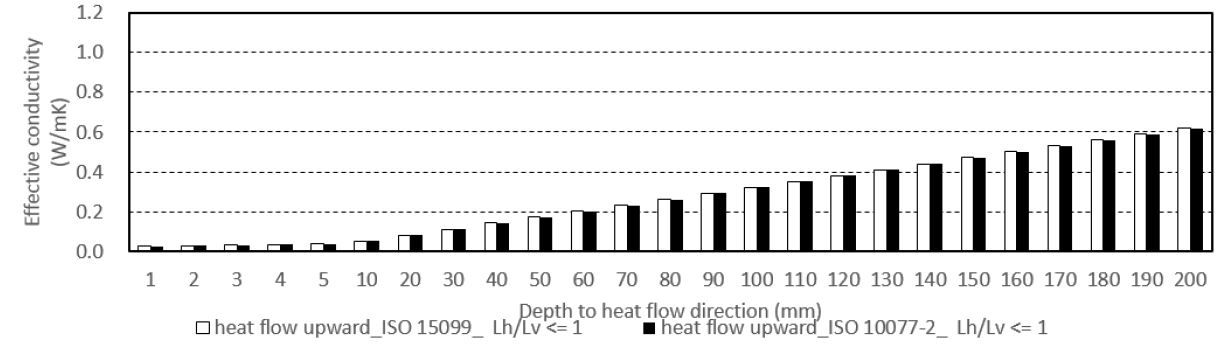
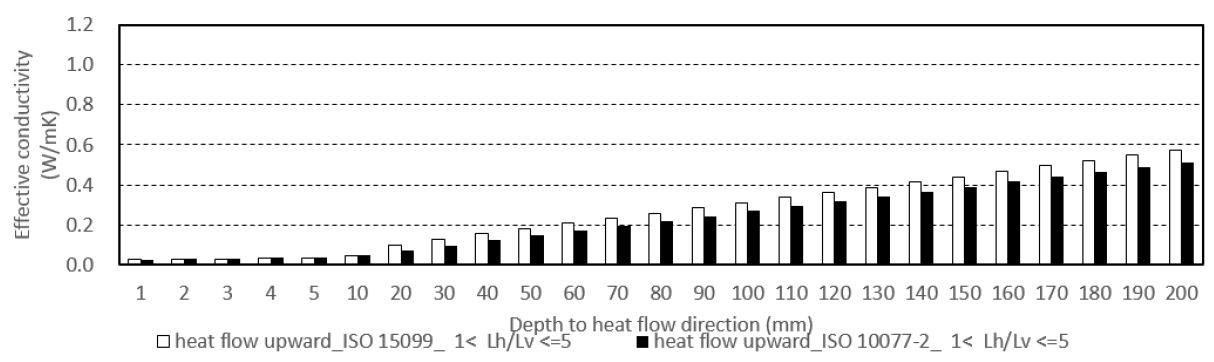
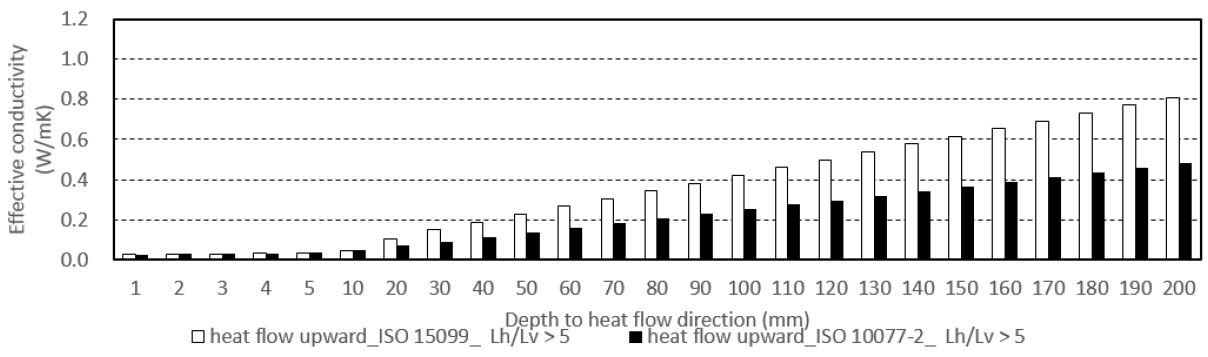
(2) 상향 열류 방향인 경우, [Lh/Lv ≦ 1] Case에서는 검토한 모든 범위에서 두 표준에 따른 유효 열전도율이 거의 같은 값을 나타내었다. [1 < Lh/Lv ≦ 5] Case에서는 열류방향 두께가 증가함에 따라 두 표준간의 차이가 발생하여 ISO 15099 산출 결과 기준으로 최대 약 27.2%까지 증가하며 전체 검토 범위에서 평균 약 10.8%의 차이가 발생되었다. 또한 [5 < Lh/Lv] Case에서는 최대 40.6%, 평균 29.6%의 차이가 발생하였으며, 두 Case 모두 대부분의 검토 범위에서 ISO 15099의 산출 결과가 높은 전도율 값을 나타내었다.
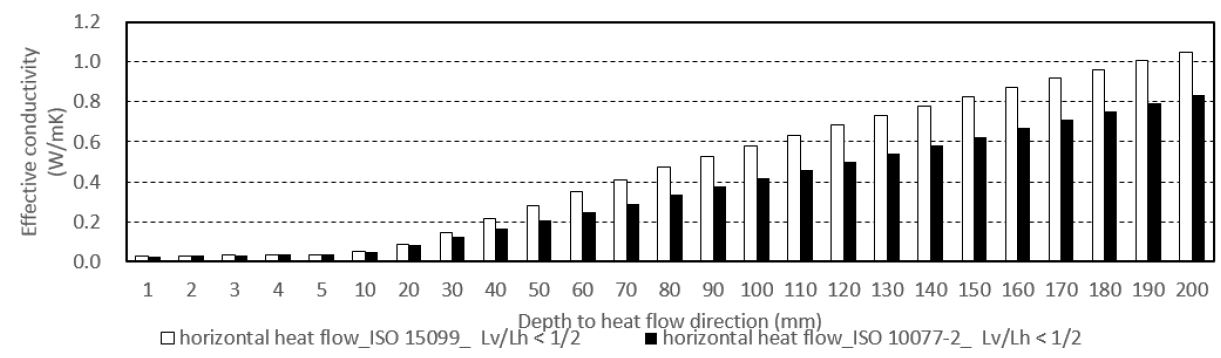
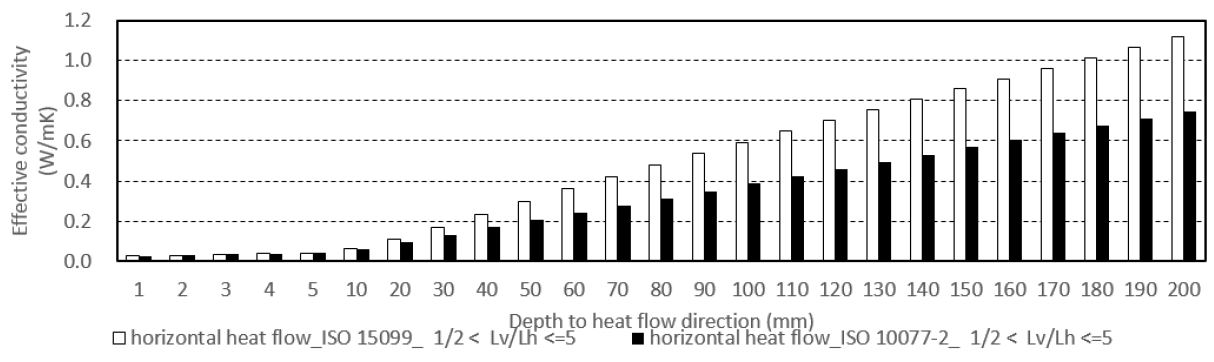
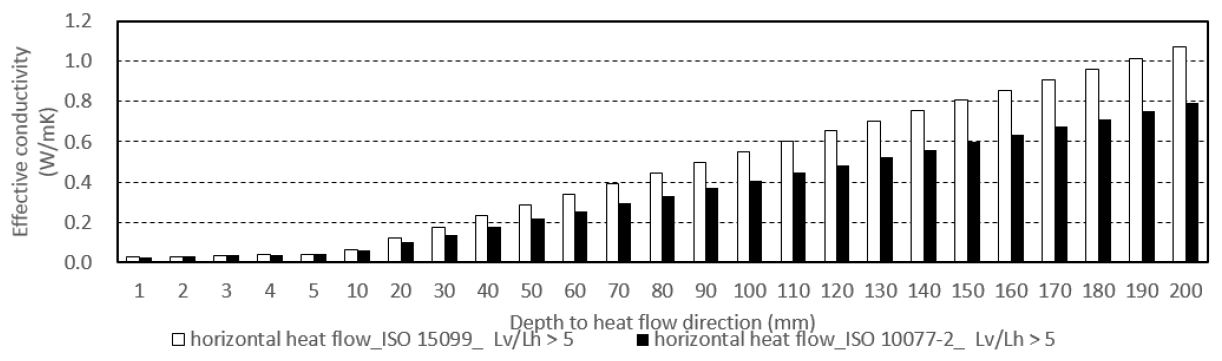
(3) 수평 열류 방향인 경우, [Lv/Lh < (1/2)]Case에서 열류방향 두께 증가에 따라 최대 29.2%, 평균 17.4%의 차이가 발생하였으며, [(1/2) < Lv/Lh ≦ 5]Case에서는 최대 34.8%, 평균 23.5%, [5 < Lv/Lh ]Case의 경우 최대 26.0%, 평균 18.2%의 유효 열전도율의 차이가 발생하였다. 거의 모든 Case에서 ISO 15099에 의한 산출결과가 ISO 10077에 의한 산출 결과보다 유효 열전도율이 높게 산출되는 것으로 나타났다.
이러한 표준별 산출 결과의 차이는 부력에 의한 대류열전달의 영향을 산출하는 방법의 차이에서 기인하는 것으로 판단되며, 열류 방향 두께(Thickness of heat flow)가 20mm 이상으로 증가하는 Case부터 표준 간 산출 결과의 차이가 급격하게 커지는 것을 볼 수 있다.
단, 산출한 유효 열전도율은 초기 조건(△K= 10)에서 산출된 값으로 실제 계산을 진행할 경우 공기층에 면한 고온과 저온측의 온도가 매 계산 단계(calculating iteration)를 지나면서 갱신되고 그에 따른 유효 열전달율을 다시 산출하여 다음 계산 단계(next iteration)에 적용하는 반복 계산을 수행하여 수렴되어야 한다.
이에, 초기 조건의 유효 열전도율이 최종적으로 계산이 완료된 이후에 수렴하여 어떻게 변화하는 지를 확인하기 위하여 별도의 열전달 해석 프로그램을 활용하였다.
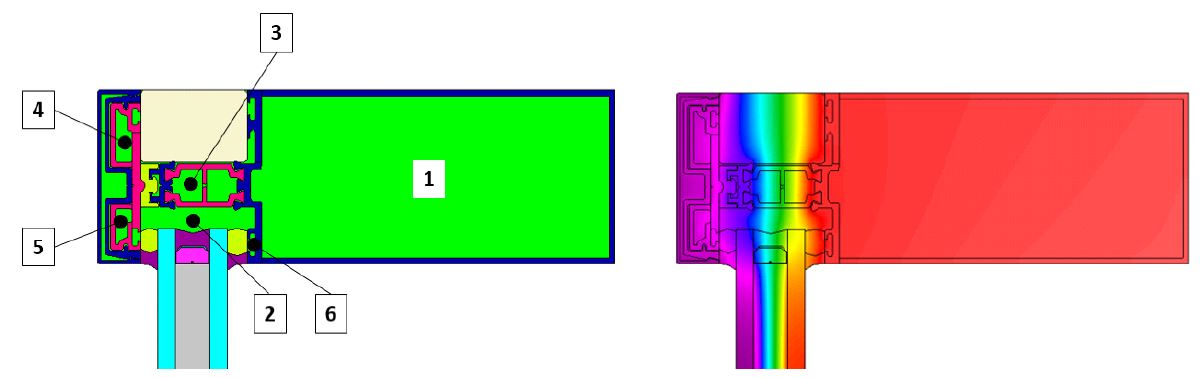
본 연구에서 활용한 열전달 해석 프로그램은 ISO 15099에 기반한 THERM(LBNL1), 미국)프로그램과 ISO 10077에 기반한 PHYSIBEL(벨기에) 프로그램으로 각 프로그램을 이용하여 다음의 Fig. 9와 같은 동일한 창호를 시뮬레이션 하여 해당 창호의 프레임 내의 공기층에 대한 유효 열전달율의 산출 결과를 계산수행 전의 초기 상태 산출값과 계산 수렴 후의 산출값을 비교하였다. 또한 각 프로그램에서 계산된 초기 조건 산출값은 ISO에서 제공하는 수식으로 별도 계산하여 비교하였으며, 비교 시 ISO 10077에 따라 공기층 형상을 간략화하여 비교 하였다.

Comparison of the effective conductivity of sample cavity according to the calculation method and process
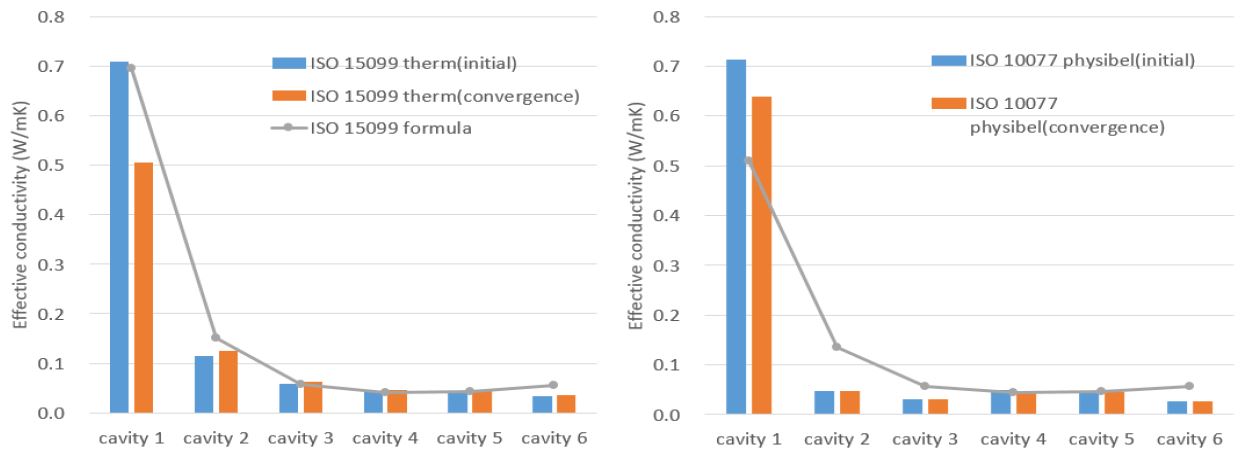
Comparison of the effective conductivity changes of sample cavity according to the calculation method process
각 프로그램에 의한 계산 수렴 후 유효 열전도율은 수렴전 값에 비하여 작아지는 경향을 나타내었으며, 각 표준에서 제시한 수식에 의하여 산출된 초기 조건의 유효 열전도율은 ISO 15099 의 경우 프로그램의 초기값에, ISO 10077의 경우 프로그램의 수렴값에 가까운 값이 산출되었다. 두 경우 모두, 표준에서 제시하는 수식에 의한 산출값이 시뮬레이션에 의한 공기층의 유효 열전도율 보다 다소 크게 평가되는 경향이 있는 것으로 판단된다.
3.3. Case별 레일리수(Ra, Rayleigh number) 비교
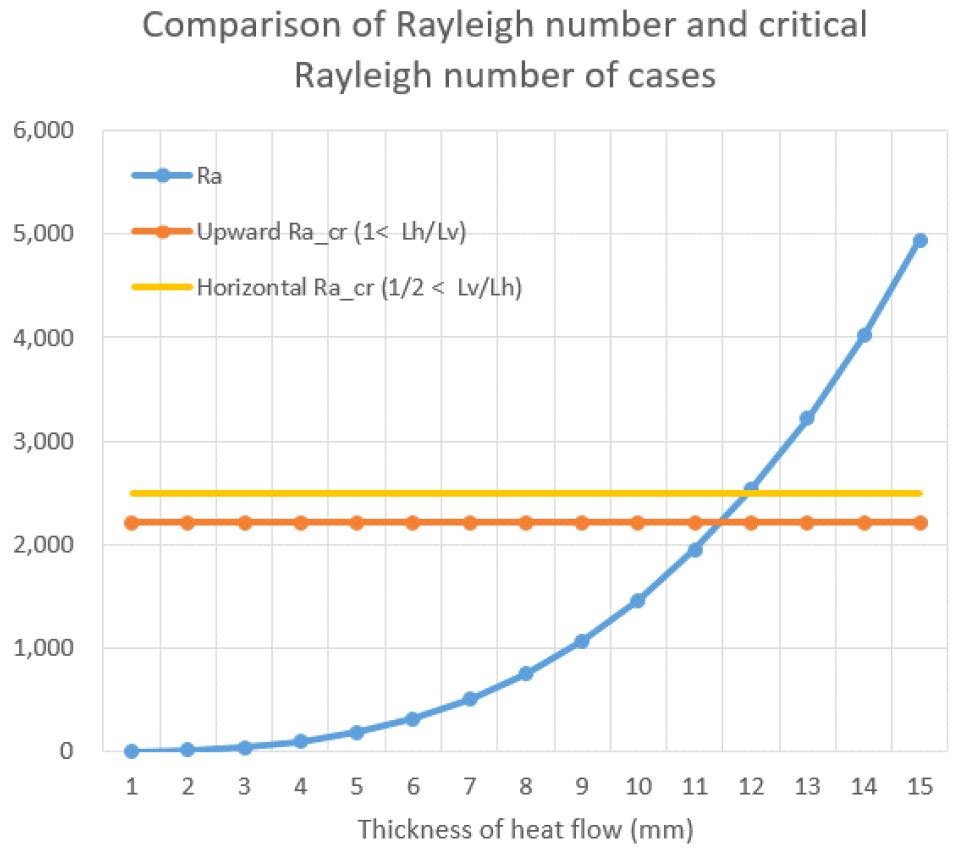
본 연구에서 비교하고 있는 두 개의 표준 중 ISO 15099에서 제시하고 있는 수식에는 레일리수(Ra, Rayleigh number)에 따라 너셀수(Nu, Nusselt number)를 산출하도록 하고 있는데, 이 때 레일리수는 공기층의 형상에 따라 대류에 의한 열전달이 주가 되는지 전도에 의한 열전달이 주가 되는지를 확인하는 지표가 된다. 본 연구에서 비교하고 있는 모든 Case에 대하여 레일리수와 임계 레일리수( Critical Rayleigh number)를 산출하여 임계수를 초과하여 대류 열전달의 영향이 강해지기 시작하는 공기층의 열류방향 두께의 범위를 확인하였다.
각 Case에 대한 분석 결과 상향 열류 방향의 경우 약 11.5mm, 수평 열류 방향의 경우 약 12.0mm의 열류방향 두께를 초과하면 대류의 영향이 커지는 것을 확인하였다.
이는 앞서 정리한 바와 같이 두 가지 표준이 제시하고 있는 유효 열전도율의 산출에서 차이가 커지기 시작하는 범위(열류방향 두께 20mm이상)와 유사하며, 대류에 의한 영향을 정밀하게 반영하기 위해서는 보다 정확한 해석 방법이 필요한 것으로 판단된다.
4. 열유동 해석을 통한 유효 열전도율(λeff) 산출
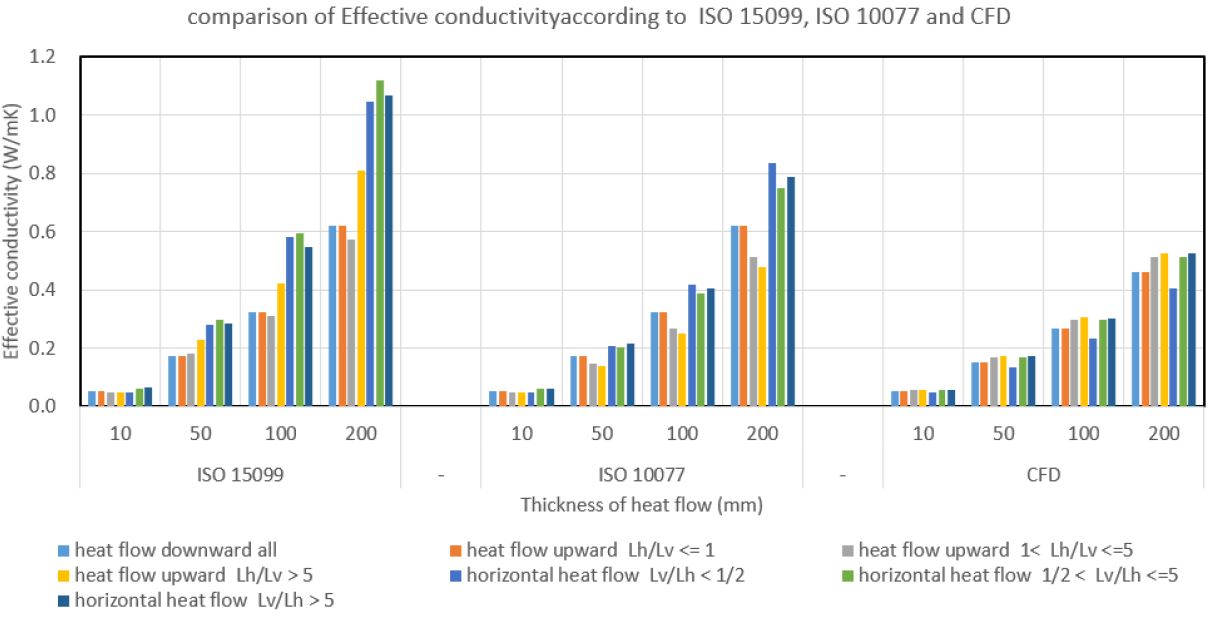
창세트 프레임 내부 공기층의 유효 열전도율을 보다 정밀하게 산출하기 위하여 CFD(Computational Fluid Dynamics) 해석을 실시하였다. 해석은 앞서 분석한 다양한 공기층 Case 중 열류방향 두께를 4가지(10mm, 50mm, 100mm, 200mm)로 제한하고 국제표준에서 제시하는 수식에서 초기 조건 유효 열전도율을 산출하는 조건과 동일한 조건을 적용하여 CFD 해석을 통한 유효 열전도율을 비교하였다.
국제 표준에서 제시하는 수식에 의한 산출결과와 CFD 시뮬레이션에 의한 산출 결과를 살펴보면 해석 Case 중 열류방향 두께 50mm이상 Case에서 각 산출방법에 따른 차이가 커지기 시작하여 ISO 15099에 의한 결과가 가장 크고, ISO 10077에 의한 결과가 ISO 15099의 결과보다 최대 약 40% 작은 값을 나타내며, 이후 CFD에 의한 산출 결과가 ISO 15099 대비 최대 약 60% 작은 값이 도출되는 것으로 확인되었다. 이는 국제 표준에서 제시한 평가 방법보다 CFD에 의한 방법이 공기층 단열성능을 다소 좋게 계산함을 의미한다.
상기의 CFD 해석 결과를 기초로 앞 절에서 비교한 알루미늄 단창의 공기층에 대한 유효 열전도율을 산정하여 시뮬레이션을 실시하였으며, 유효 열전도율 산정 시 공기층의 열류방향 두께가 작아서 대류 영향이 적은 경우는 그대로 ISO 15099의 산정 방법을 활용하는 것으로 하였다. 이와 같이 도출된 유효 열전도율을 THERM 프로그램에 반영하여 창세트의 전체 열관류율을 분석하였으며, 분석된 결과는 동일한 창세트에 대한 물리적 시험 결과와 비교 분석 하였다.

Comparison of the effective conductivity( λeff) changes of sample cavity according to the calculation process
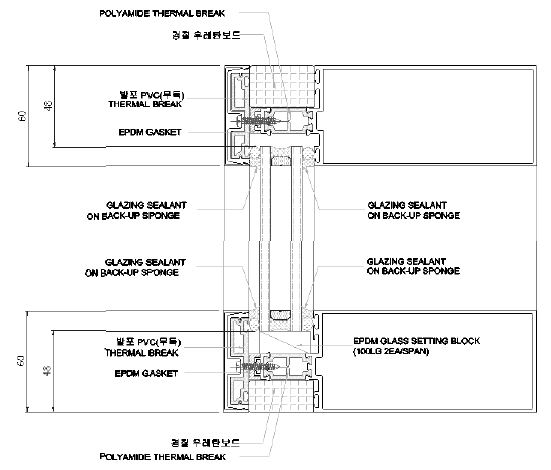
다음의 Fig. 13과 Fig. 14는 대상 창세트에 대한 형상을 알 수 있는 단면과 해당 창세트에 대한 실물 실험 장면이다. 대상 창세트에 대한 실물 실험은 KS F 2278을 활용하여 실험을 진행하였으며, 이에 따라, 비교 시뮬레이션도 KS에 규정된 경계조건을 적용하였다.
실물 실험 결과와 ISO 15099에서 제시한 유효 열전도율을 적용한 경우, 그리고 CFD 해석 결과에 기초한 유효 열전도율을 적용한 경우를 비교한 결과, CFD 해석을 활용하면 실험 결과와 시뮬레이션 결과의 오차를 다소 감소시킬 수 있는 것으로 나타났다.
5. 결론
창틀 내부의 공기층에 대한 물성을 산출하는 두 가지 국제 표준상의 방법과 보다 정밀한 방법인 CFD 해석의 결과를 이용하여 창틀 내부 공기층의 유효 열전도율을 산출하여 비교한 결과, 초기 조건에 따른 유효 열전도율 산출값은 ISO 10599, ISO 10077, CFD해석 결과의 순으로 작은 값을 도출하였으며, 계산을 통해 유효 열전도율이 수렴된 값은 ISO 10077, ISO 15099, CFD 해석 결과의 순으로 작은 값이 도출되었다. 이는 기존의 해석 방법이 공기층 단열성능을 상대적으로 열악하게 산출하고 있음을 나타낸다. 이에 동일한 창호의 프레임 내부 공기층에 대하여 CFD 해석 결과에 기초한 유효 열전도율과 ISO 15099에 기초한 유효 열전도율을 각각 적용하여 창세트 열관류율을 시뮬레이션하고 이 결과를 실물 실험결과와 비교한 바, CFD 해석 결과를 반영함으로써 실물 실험과 시뮬레이션 결과의 오차를 다소 감소시킬 수 있는 것으로 나타났다. 향후 공기층 물성에 대한 보다 정확한 해석 방법의 개발을 위한 기초 자료가 될 수 있을 것으로 사료된다.
Nomenclature
| d : | 열류방향 공기층 두께 (m) |
| hcv : | 대류 열전달 계수 |
| hr : | 복사 열전달 계수 |
| Lh : | 공기층 단면의 길이 |
| Lv : | 공기층 단면의 높이 |
| Nu : | 너셀 수(Nusselt number) |
| Ra : | 레일리 수(Rayleigh number) |
| Racr : | 임계 레일리 수(Rayleigh number) |
| Rs : | 공기층의 열전도저항 |
| λai : | 공기의 열전도율 |
| λeff : | 창틀의 유효 열전도율(W/mK) |
Acknowledgments
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning(KETEP) and the Ministry of Trade, Industry & Energy(MOTIE) of the Republic of Korea (No. 2015000000210).
Notes
References
- ISO, ISO 15099:2003(E) Thermal performance of windows, doors and shading devices - detailed calculations, (2003).
- ISO, ISO 10077-1:2006(E) Thermal performance of windows, doors and shutters - Calculation of thermal transmittance part 1: General, (2006).
- ISO, ISO 10077-2:2012(E) Thermal performance of windows, doors and shutters - Calculation of thermal transmittance part 2: Numerical method for frames, (2012).
-
KS, KS F 2278:2014 창호의 단열성 시험방법.
KS, KS F 2278:2014 Standard test method for thermal resistance for windows and doors. - Arild Gustavsen PhD, et al , "Experimental and Numerical Examination of the Thermal Transmittance of High Performance Window Frames", (2010), ASHRAE.