벽면 온도차가 있는 공기층의 경사각에 따른 자연대류 열유동
Abstract
The smart façade system which is under development consists of a curtain wall unit, a heat exchanger unit, and a heat collection unit with a heat storage and circulation. Using the effective thermal conductivity of the air layer in ISO15099 is insufficient to predict the heat transfer of air cavity in the smart façade system. In order to improve the prediction, a heat and flow analysis code instead of effective thermal conductivity is employed. The changes in heat transfer rate and flow characteristics according to the inclination of the device were identified.
We developed a thermal flow analysis code to calculate and analysis easily the air layer in the smart façade system. The code employed the Boussinesq approximation for buoyancy, SIMPLE method for imcompressible flow, and unstructred grid system.
Calculations were performed for cases where the longitudinal (x-axis) and the width (y-axis) directions were tilted. There was little change in heat flow in the y-axis inclining and there was relatively no significant changes in the x-axis below 10 degrees. However, when the inclined angle exceeded -50 degrees, there is a change in flow characteristics and the heat exchange is significant. Based on the results of the analysis, when installing the smart envelope, it must be within 10 degrees to sustain the designed performance.
Keywords:
Natural Convection, Numerical Analysis, Inclined Angle키워드:
자연대류, 수치해석, 경사각1. 서론
1.1. 연구의 배경 및 목적
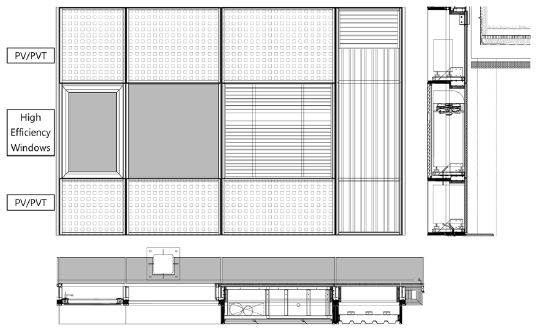
제로에너지 건축물 구현을 위한 수요에 대응하기 위하여 건물의 다양한 외장재, 설비/신재생 요소기술을 융합하여 확장성능을 지닌 외장재 융복합시스템(IUES, Incremental Unitary Envelope System)의 개발이 진행 중이며, 개발 외피의 구성(Fig. 1.)은 커튼월 프레임에 투명 및 불투명의 고단열 외피로 구성되는 커튼월 유닛과 냉난방, 열교환 환기 설비유닛, 축열체와 열매 순환 구조로 구성된 집열 유닛으로 되어 있다. 커튼월 유닛과 설비 유닛의 불투명 구간에는 PV 및 PVT를 설치하여 신재생에너지를 생산할 수 있도록 하였다. IUES 시스템을 건물에 적용하기 위해서는 설치 후 시스템 성능을 예측할 수 있는 평가 기법 및 도구가 필요하다. 기존의 ISO 15099에 기반한 열전달 해석법을 활용하여 IUES 시스템의 열성능 해석을 수행하는 방안을 검토하였으나 내부 설비의 발열, 대류(강제대류, 자연대류)에 의한 유동의 영향을 받는 공기층이 존재하여 해당 영역을 단순 공기층과 같이 유효 열전도율을 반영한 전도(conduction)로 열 해석하는 것은 부적합하며, 해당 구간에서 설비 운전에 따른 IUES 유닛 내부의 열과 유동을 동시에 고려한 열유동을 해석하여야 타당한 열성능 분석이 가능하다.
IUES 시스템은 한정된 유체 영역 내부에서 대류에 의한 유동의 발생과 설비의 발열이 해석 영역 내부의 열유동을 결정하는 주된 요소로 판단되며, 이에 따라 개발되는 해석 모델도 외피 시스템 내부의 한정된 공간을 해석 대상으로 개발하였으며, 기존의 열전달 해석 모델과 통합하여 평가 대상인 IUES 시스템에 대하여 연성 해석을 수행할 수 있는 코드를 개발하였다. IUES는 크게 팬을 이용한 강제대류와 추가적인 에너지를 사용하지 않는 자연대류를 이용하는 두 가지의 운전 모드가 있다. 본 연구는 IUES 시스템에 열유동 해석 코드를 적용하기 위한 중간 단계로 IUES 시스템을 건물의 외벽에 설치할 때 자연대류운전 모드에서 기울어지게 설치되는 패널(BIPV 등)에 의한 기울어진 면에 접하는 공기층의 열전달 변화에 대한 수치해석을 수행하였다.
1.2. 수치해석을 통한 자연대류 연구
자연대류 현상을 이용한 방열 장치는 휜(fin)구조를 이용하여 대류를 높여 열전달을 높일 수 있다. Hagighi et al.[1]는 자연대류에 의한 열전달 기구인 plate-fin구조에 cubic pin-fin을 추가하여 열전달을 높이는 실험적 연구를 수행하였다. 판(plate)만으로 구성된 plate-fin 구조에 판 사이에 1개의 판을 cubic pin-fin으로 변경하였다. 이를 통해 자연대류의 효과가 증가하고 열전달율이 증가하였다.
유체에 팬과 같은 강제적 방법으로 유동을 유도하지 않아도 유체에 잠긴 고온의 물체는 주변 유체의 온도를 바꾸어 유체 밀도 변화로 상승하거나 하강하는 유동을 발생하게 된다. Sparrow and Stretton[2]는 고온의 정육면체를 다양한 각도로 기울여 자연대류에 의한 열전달 현상을 물과 공기 중에서 관찰하였다. 물과 공기를 사용하므로 여러 Rayleigh 수에 관해서 실험할 수 있었다. 그러나 이 두 자료는 서로 약간의 차이를 보였고 새롭게 제시한 길이(투영된 면적에 제곱근을 취한 새로운 길이)를 사용하여 Rayleight와 Nu수의 관계가 비교적 잘 일치하는 것을 확인하였다.
Cha and Cha[3,4]는 대공간 속에 일정한 온도로 유지되는 육면체가 자연대류에 의해 열에너지가 전달되는 현상을 수치적인 방법으로 연구하였다. 여러 Rayleigh수에 따라 계산을 수행하였다. Rayleigh수가 낮을 때는 육면체의 아래 면에서 많은 에너지전달이 발생하였으나 Rayleigh가 올라가면서 높은 에너지전달이 옆면으로 옮겨가는 현상을 발견하였다. 비압축성 유체를 해석하기 위하여 SIMPLE방법을 사용하였으며 정렬격자에서 사용하는 수치해법으로 TDMA(Tridiagonal matrix algorithm)을 사용하였다. Cha and Cha는 2개의 육면체의 상호작용에 의한 열전달 현상으로 연구를 확장하였다. 또한 실험을 통하여 수치해석 방법을 검증하였다. 1개의 육면체에 비하여 2개의 육면체일 때 각각 육면체의 Nu수는 더 작아지며 두 육면체의 거리가 가까울수록 열전달이 감소한다고 하였다. 특히 높이에 차이기 있도록 대각선으로 놓인 두 육면체 중 아래쪽에 있는 육면체의 열전달이 위쪽에 있는 육면체에 비하여 열전달율이 감소하는 것을 확인하였다.
자연대류는 고체와 이에 접한 유체 사이에 에너지전달이 발생하고 에너지를 얻은 주변의 공기는 부력에 의해 상승하게 된다. 고체와 유체가 상호작용하게 되므로 고체와 유체를 동시에 고려한 해석이 필요하다. Lee and Lee[5]는 자연대류에 있어서 유체-고체를 동시에 포함한 수치해석을 수행하였다. 동일한 유동 공간을 가진 영역에 알루미늄, 벽돌, 나무, 단열재와 같이 건축에 많이 사용되는 재료를 고체로하여 계산을 수행하였다. Rayleigh수가 1×105에 이르면 전도에서 대류로 지배적인 에너지전달 메커니즘이 변경되는 것을 확인하였다.
밀폐된 공간에 공기와 고온의 물체가 놓이는 경우 중력에 의해 상승하는 기류가 발생하지만, 밀폐된 공간으로 인해 유체는 다시 하강하고 내부에 순환하는 유동이 발생한다. 벽면이 단열이 아닌 경우 시간이 지남에 따라 일정한 유동 형태를 보이게 된다. Kim et al.[6]은 밀폐된 공간에 수평으로 2열의 실린더가 무한히 놓여 있는 형상을 수치 해석하기 위하여 4개만을 포함한 공간과 반복 경계(periodic condition)를 사용하여 구현하였다. 실린더 형상을 구현하기 위하여 가상경계법(immersed boundary method)을 사용하였다. 열유동에 많은 영향을 미치는 요소는 실린더 간의 거리라고 하였으며 거리가 멀어질수록 열전달율이 높아진다고 하였다.
2. 수치해석의 이론과 검증
2.1. 전산역학 모델 : 유동방정식과 유한체적법
유체는 비압축성, 뉴턴유체로 가정하여 다음의 연속, N-S, 에너지 방정식을 사용하였다.
| (Eq. 1) |
| (Eq. 2) |
| (Eq. 3) |
여기서 ρ는 밀도(kg/m3), 는 속도벡터(m/s), 는 중력가속도(m/s2), p는 압력(Pa), 는 응력텐서(Pa), cp은 정압비열(J/(kgK)), T는 온도(K), k 열전도계수(W/(mK)), Φ는 점성소산(J/s), 는 에너지 생성항(J/s), t시간(s)을 의미한다. 에너지 방정식은 여러 가지 형식으로 표현할 수 있으나 본 연구에서는 비압축성 유체로 생각하여 온도에 관한 식을 사용하였다. 연속방정식 (Eq. 1)은 비압축성이면 시간 항이 없어지며 속도에 관한 제한값(constraint)과 같은 역할만을 하게 된다. 이는 닫힘 문제가 되기 위한 방정식 1개가 부족한 상황이 되며 이를 극복하기 위하여 SIMPLE방법[7]을 사용하였다. 본 연구에는 포함하고 있지 않지만, 사용한 프로그램은 유체와 고체의 열과 온도를 동시에 해석할 수 있도록 개발되었으며, 고체에 관해서는 유동이 없으므로 에너지 방정식에서 왼쪽의 대류항이 없는 식을 사용하였다.
(Eq. 1)-(Eq. 3) 방정식은 (Eq. 4)와 같이 적분방정식으로 표현할 수 있으며 적분방정식을 차분화하여 각 셀(cell)마다 적용하여 미지 값(속도, 온도, 압력)을 구할 수 있는 대수방정식을 얻는 유한체적법(FVM, finite volume method)을 사용하였다. 유한체적법으로 차분화한 식은 컴퓨터로 쉽게 계산할 수 있는 연립방정식이 되며 이 연립방정식을 풀어 해를 구하였다.
| (Eq. 4) |
(Eq. 4)에서 ϕ는 종속변수(속도, 운동량, 온도), V는 검사체적(m3)의 부피 S는 검사체적의 표면적(m2), v는 좌표계에서의 절대속도(m/s), vs는 검사표면의 속도 벡터(m/s), Γ는 확산계수, Qϕ는 원천(source)항을 나타낸다. (Eq. 4)의 좌변은 시간에 따른 변화를 의미하는 비정상항(unsteady state)와 유체가 이동하면서 전달하는 대류항(convection)을 나타낸다. 본 연구에서 독립변수인 스칼라 함수는 x, y, z에 따른 속도 성분(u, v, w), 온도(T), 압력(p)이 된다. 각 항을 차분화해야 하며 이 중 대류항은 정밀도와 안정성을 고려해서 다음(Eq. 5)과 같이 1, 2차 정밀도를 섞은 형태를 사용하였다.
| (Eq. 5) |
하첨자 P0는 격자점에서 값이며, Pj주변격자에서의 값을 나타낸다. J는 면 통과량(flux)을 의미한다. 확산항은 격자 사이 면에서의 구배 값을 필요로 한다. 구배는 다음(Eq. 6)과 같이 구하였다.
| (Eq. 6) |
하첨자 j면에서 값을 의미하며 S,ds 는 면벡터와 셀 중심에서 면까지의 거리를 나타내는 벡터이다.
Ra수(Rayleigh수)와 Nu수(Nusselt수)는 다음(Eq. 7)과 같다.
| (Eq. 7) |
여기서 g, β, ν, α는 중력가속도(m/s2), 열평창계수(1/K), 동점성계수(m2/s), 열확산계수(k/ρcp, m2/s)를 각각 나타낸다. L, Th, Tc, Δn은 대표길이, 고온 면의 온도, 저온 면의 온도, 경계면에서 수직거리를 나타낸다. Nu수는 평균 Nu수를 나타낸다. 부력은 비압축성 유동으로 가정하였기 때문에 다음(Eq. 8)과 같이 Boussinesq 방법 (Boussinesq approximation)[8]을 사용하였다.
| (Eq. 8) |
ρ0는 참고 밀도로 T0온도일 때 밀도를 나타낸다.
2.2. 수치모델 검증(validation)
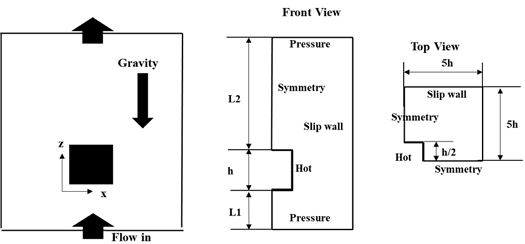
먼저 본 연구에서 개발한 코드가 자연대류에 의한 유동과 온도를 적절하게 모사하는지 확인하기 위하여 고체가 일정한 온도로 유지되고 부력으로 상승하는 유동에 관하여 참고 문헌[9]과 비교하였다. 계산 영역은 Fig. 2.과 같다. 중력 방향은 -z 방향이며 상부와 하부는 공기가 부력에 의해 자연스럽게 들어오고 나갈 수 있도록 압력 경계(pressure boundary)를 사용하였다. 계산 영역은 h=0.04m, L1 = 0.1m, L2 = 0.46m을 사용하였다.
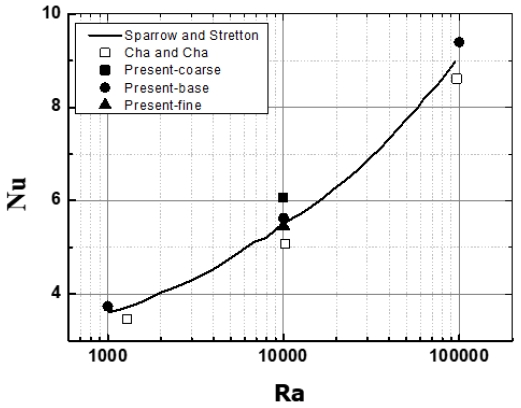
Sparrow and Stretton[2]의 실험과 Cha and Cha[3]의 수치 계산한 결과를 Fig. 3.에 표시하였다. 본 연구에서는 정적 계산(steady state calculation)을 수행하였다. 격자의 수 16000, 31100, 55500개로 바꾸어 가며 계산을 수행하였으며 이에 따라 해가 수렴하는 것을 확인할 수 있다. 본 연구의 결과가 전체적으로 Sparrow and Stretton의 실험과 잘 일치하는 것을 확인할 수 있다.
3. 계산 결과 및 분석
3.1. 수치해석 영역
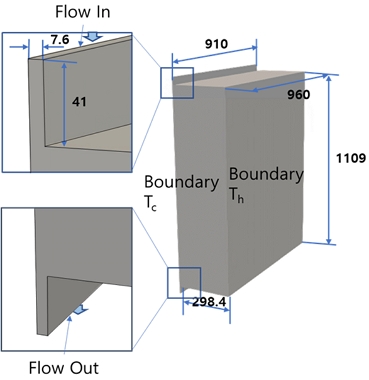
IUES 시스템 중 공기의 대류에 의한 에너지를 교환하는 부분만을 따로 축출하여 수치해석을 수행하였다. 계산 영역의 전체적인 형상은 Fig. 4에 표시하였다. 전면부는 주로 일사에 의해 열에너지를 받아 고온(Th)을 유지하는 부분이며 후면은 실내와 접한 면으로 낮은 온도(Tc)가 유지된다. 실내/외에 접한 면들(고온부와 저온부)의 온도는 일정하게 유지된다고 가정하였다.
Fig. 4.를 보면 후면부에 접한 상부와 하부에 공기가 들어오고 나갈 수 있는 입출구 얇은 슬릿 형태로 되어 있다. 전면이 고온부이기 때문에 상부의 슬릿에서는 유입이 발생하고 하부에서는 유출이 발생한다. 그 외의 영역은 단열 조건을 사용하였다. 벽면의 온도차이(Th - Tc)는 20도가 되도록 하였다. 물성치는 공기를 사용하였으며 Ra =3.4×105이 되도록 밀도를 조정하였다.
격자 의존성(mesh dependency)을 확인하기 위하여 격자의 개수를 14,900(coarse), 36,400(base), 68,832(refine)개로 늘리면서 벽면에서의 Nu수를 비교하였다. 사용한 격자는 Fig. 5.와 같으며 벽면의 온도와 유속의 구배를 고려하여 벽면에 크기가 작은 격자가 들어가도록 하였으며 구배가 작은 중심부는 상대적으로 큰 격자를 사용하였다. 격자는 열해석 프로그램인 ICE[12]를 이용하여 생성하였으며 생성된 격자구조를 읽어 열유동 해석을 수행하였다. ICE에서 생성한 격자는 전체가 육면체로 되어 있다. 가장 많은 격자수를 갖는 격자에서 얻은 Nu수에 대하여 성긴 격자와 기본격자에서 얻어진 Nu수의 상대 오차를 비교하였다. 그 값을 Table 1.에 나타내었다. 성긴 격자에서 상대 오차는 0.82%, 기본격자는 0.19%로 기본격자뿐 아니라 성긴 격자에서도 충분히 정밀한 계산이 이루어지고 있는 것을 알 수 있다. 본 연구에서는 계산의 효율과 정밀도를 고려하여 이후 모든 계산은 기본격자인 36,400개의 격자를 사용하여 계산을 수행하였다.
3.2. 결과 및 분석
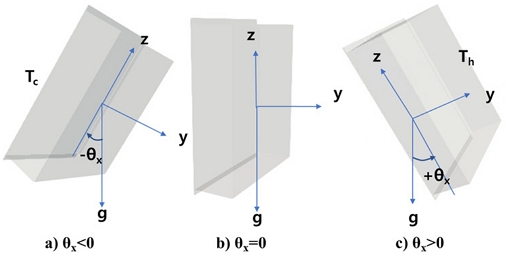
IUES의 시스템 내부 공기층은 내부에 설치되는 설비 또는 패널의 설치 조건에 따라 중력에 나란하지 않은 기울어짐이 발생할 수 있으며 이러한 기울어짐이 있는 벽면을 통한 에너지의 수수를 수치적 방법으로 관찰하였다. 공기층의 좌표와 중력의 방향은 Fig. 6.과 같다. 두께 방향은 y방향으로 하였으며 폭은 x방향에 나란하다. z방향은 높이 방향으로 하였다. 기울어지지 않은 공기층(Fig. 6. b))는 z방향이 중력과 나란하며 방향은 서로 반대이다. z방향은 상부로 향하고 중력은 –z방향으로 하였다. 공기층의 기울어짐은 x축, y축을 회전축으로 기울어지도록 하였다. Fig. 6.은 x축을 기준으로 기울어진 형태를 나타낸다. 각도는 θx로 나타내었다. 반시계 방향을 양(+)로 하였으며 시계방향은 음(-)으로 하였다. θy방향 기울어짐은 그림으로 나타내지 않았으나 축이 y인 것을 제외하고는 Fig. 6.과 같다.
중력은 그림에서 나타낸 것과 같이 수직 아래 방향으로 작용한다. 계산의 편의성을 고려하여 공기층은 그대로 두고 중력 벡터의 방향을 적절히 변경하여 계산을 수행하였다. Fig. 6. a)는 음의 기울기를 가진 경우로 표면 온도가 Tc인 낮은 온도를 가진 벽면이 상부로 놓이게 되며 고온부인(Th) 벽면이 하부에 놓이게 된다. Fig. 6. c)는 양의 기울기를 나타내며 중력 방향이 반대가 된다. 이에 따라 Fig. 6. c)는 Tc면보다 Th인 벽면이 더 중력에 대하여 위쪽에 놓이게 된다. 고온부의 상부에 “ㄱ”자로 꺾이는 공간이 발생하고 유동이 자연스럽게 빠져나가지 못하고 유속이 느려지고 대류가 감소며 열전달이 감소하게 된다. Fig. 6. a)는 반대로 상승하는 기류가 자연스럽게 빠져나갈 수 있게 되면서 대류가 강화되어 열전달이 향상된다. 다른 한편 기울어짐이 y축을 기준으로 일어나는 경우, Th와 Tc인 벽면이 중력에 대하여 상대적인 위치의 변화가 없어 중력의 영향이 비교적 적을 것을 예상할 수 있다.
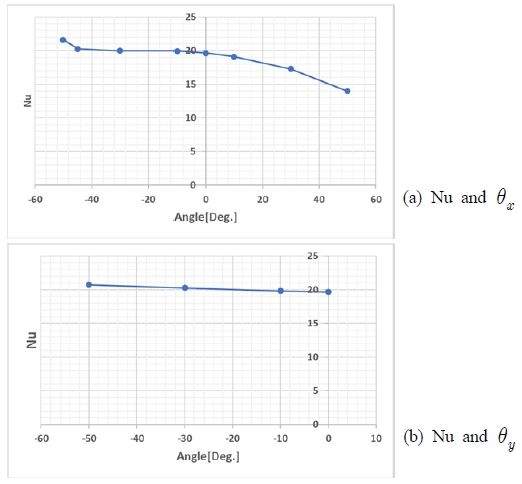
Fig. 7.은 공기층의 기울어짐(θx, θy)에 따라 Nu수의 변화를 나타내었다. Fig. 7. (a)는 x축을 회전축으로 기울어진 각도에 따른 공기층의 Nu수를 나타낸다. Fig. 7. (b)는 y축을 기준으로 기울어짐에 따른 Nu수이다. Fig. 7. (b)는 중력 방향과 고온면, 저온면이 이루는 각도가 기울어지는 각도에 무관하게 변화하지 않기 때문에 열유량은 각도에 무관하게 거의 일정한 값을 나타내고 있다. 반면에 θx의 변화에 대해서는 중력과 벽면의 각도가 달라져 부력에 의해 상승하는 기류가 영향을 받게 된다. 그러므로 θy에 비하여 θx의 변화에 민감하게 열전달율이 변하게 된다. 입구와 출구 슬릿은 낮은 온도를 갖는 면에 접해 있으므로 상부의 슬릿에서 유동이 들어오고 하부의 슬릿으로 유동이 나가게 된다. 입출구 슬릿을 통과하는 유속의 크기는 O(10-6)의 크기를 가지며 내부 공기층의 속도가 O(10-2)인데 비하여 매우 작아 입출구 슬릿을 통과하는 유동에 의한 고온부와 저온부를 통과하는 열유동에 미치는 영향은 매우 작은 것으로 생각된다. 슬릿을 통과하는 유량이 적은 것은 슬릿의 폭이 매우 작아 점성이 지배적으로 작용하기 때문으로 생각된다.
Fig. 7. (a)에서 공기층의 기울어진 각도에 따라 중력과 고온면, 저온면의 기울기가 달라져 경계층이 변하고, 상부의 정체 구간에 의해 공기의 흐름이 달라져 벽면을 통한 열유량이 바뀌게 된다. 양의 각도(θx)로 기울어질수록 열유량은 각도에 비례하여 감소한다. 반대로 음의 각도로 기울어 경우, 각도가 작을 때는 일정하게 유지되지만 45도보다 큰 경우 열유량의 급격하게 증가하는데 이는 유동 특성이 달라지기 때문으로 생각된다. 우선 양의 각도로 기울어지는 경우를 생각해 보자. 기울어진 각도가 양수인 경우 Th온도를 갖는 벽면이 상부로 가고 Tc면은 하부로 가게 되어 부력의 효과가 감소할 뿐 아니라 0도인 경우에 비하여 공기층의 상부에 단열면은 문턱과 같은 원할한 유동을 방해하는 공간이 발생하여 각도가 커짐에 따라 열유량이 낮아진다. 반대로 음의 각도를 가지는 경우 Tc가 상부로 가게 되며 Th가 하부에 놓이게 되어 정체 구간이 줄어들고 공기층 상부에 유동이 원활하고 중심에 정체 구간이 줄어들어 열전달률이 약간씩 늘어나게 된다.
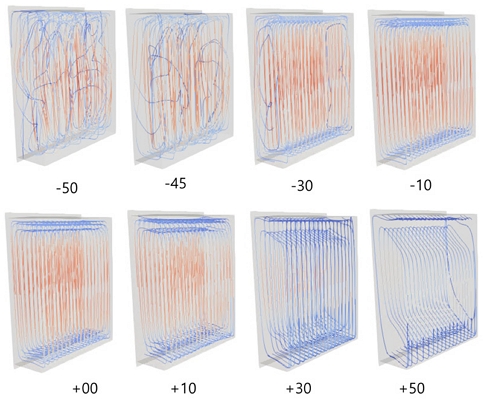
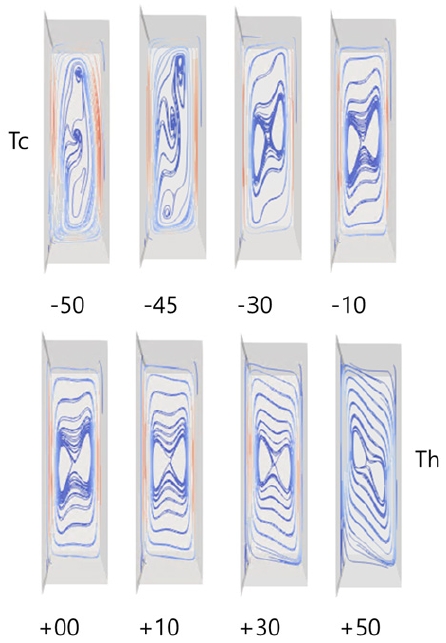
Fig. 8.은 공기층 내의 전체적인 유동(stream line)을 보여준다. 기울어지는 각도가 θx > 30경우와 θx < -30경우 확연한 차이를 보인다. -10 ≦ θx ≦10에서는 유동의 차이가 거의 없으며 유사한 것을 알 수 있다. 이 구간에서는 중심부에 정체 구간이 있으며 고온벽면(Th)을 따라 올라간 공기는 상부 가장자리 가까이까지 이른 후에 상부 벽을 따라 왼쪽으로 이동하고 이후 저온 벽면(Tc)을 만나 하강하는 유동이 발생한다. +30 ≦ θx ≦ +50에서는 확연하게 공기층 상부에 정체되는 구간이 증가하고 내부 순환 영역이 줄어든 것을 알 수 있다. 상부 가장자리는 중력을 생각해 보면 저온부에 접한 면이 약간 내려오는 형상을 가지며 문턱과 같은 역할을 한다. 이 문턱은 원활한 공기의 흐름을 방해한다. 각도가 커짐에 따라 더 큰 문턱이 된다. θx = 50에서 가장 심하게 나타나며 이에 따라 유동이 원활하지 않고 열전달이 급격히 감소하게 된다. θx = -30~-50까지 보면 다른 경우와 다르게 측면에서 3차원 유동이 발생하는 것을 알 수 있다. θx = -30에서는 3차원 유동이 끝단에 국한적으로 발생하고 있으며 열전달율에는 영향을 미치지 않는다. θx = -50에서는 급격하게 3차원 효과가 늘어나고 중심부 일부를 제외하고 전체적으로 나타나고 있다. Th면을 따라 상부로 올라가는 유동 이외에 2차 유동이 발생하며 유동 특성이 달라진다. 이에 따라 급격하게 열전달율이 증가하고 있다.
Fig. 9.는 길이 방향(x)의 중심부에서 유선을 기울어짐 각도 변화에 따라 보여준다. 색상은 속도의 크기를 나타낸다. θx = 0일 때 오른쪽 면의 높은 온도로 인해 상승하는 기류가 발생하고 왼쪽 면의 낮은 온도로 인해 하강하는 기류가 생긴다. 중심부에 정체 구간이 나타나는 전형적인 자연대류 현상을 보여주고 있다. 상승하는 기류로 인해 중심부 정체 구간의 오른쪽은 위로 치우쳐져 있으며 왼쪽은 하강하는 기류로 인해 아래로 치우쳐져 있다. 속도가 느려지는 구간 없이 상부에서 자연스럽게 빠져나가는 것을 확인할 수 있다. θx > 0으로 기울어짐에 따라 공기층의 상부와 하부에 대칭적으로 속도가 느려지는 부분이 발생하며 중심부의 정체 구간이 θx = +10도에서 거의 대칭적인 모양을 나타내며 각도가 더 커짐에 따라 오른쪽에서 오히려 아래로 치우쳐지며 왼쪽은 위쪽으로 치우쳐진다. 상부의 저속구간은 2차유동(secondary flow)이 발생하는 정도는 아니며 유속이 급격하게 느려져 천천히 왼쪽으로 이동하게 된다. 상하부에 정체 구간은 기울어짐에 의해 문턱처럼 작용하여 이를 넘기 위해서는 더 많은 운동에너지가 있어야 한다. 기울어진 각도(-30 ≦ θx ≦30)가 증가해도 2차원 유동(x방향 유동 속도는 거의 0)을 유지한다. θx = -45가 넘어가면 경계층 내의 유속이 증가하고 양쪽 끝에서 중심으로 향하는 3차원 유동이 발생하며 중심의 정체 구간이 줄어든다. θx = -50의 경우 고온면이나 저온면을 따라 흐르는 유동 이외에 2차 유동이 발생하며 이에 따라 열유동이 증가하게 된다.
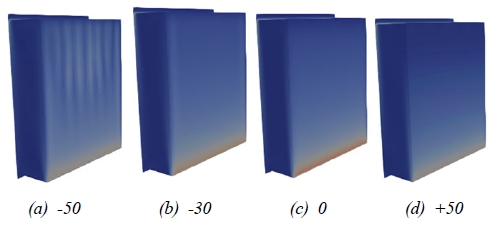
Fig. 10.은 벽면에서 온도 구배(temperature gradient)를 기울어진 각도에 따라 표시하였다. 온도 구배는 열전달과 직접적인 관계가 있는 값으로 벽면을 통하여 전달되는 열전달양을 확인할 수 있다. 전체적으로 고온면의 하부가 다른 면에 비하여 큰 값을 가고 있는데 이는 Tc의 온도를 갖는 벽면을 따라 하강한 기류가 아래 벽면을 통해 고온부로 유입되기 때문에 새로 유입되는 공기는 낮은 온도를 유지하고 있어 구배가 커진다. θx = +50의 경우 아랫부분에 저속구간이 생기고 유동이 원활하지 않아 다른 각도에 비하여 낮은 값을 나타내는 것을 확인할 수 있다. Fig. 10. (a), (b) 아랫부분에서 Fig. 10. (c)의 0도에 비하여 적은 값을 보이고 있지만 고온벽면 전체적으로 증가하고 있다. 또 Fig. 10. (a)에서는 지역적으로 2차 유동 즉 3차원 유동의 현상들이 나타나며 국소적으로도 변화하는 것을 알 수 있다. 이러한 3차원 유동은 상하부에 저온 고온을 가지고 있는 자연대류에서 발생하는 Bernad cell [11]과 유사한 모양을 나타내고 있다. 이러한 3차원 현상은 열전달율을 증대시키는 주요한 원인이라고 생각되며 향후 이에 관한 추가적인 연구가 필요하다.
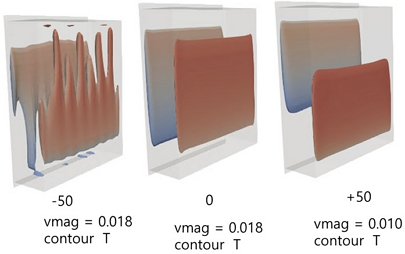
Fig. 11.은 공기층 내부의 등온도면(Iso-surface)이다. -30 ≦ θx ≦ +50 및 θy = 30에서 공기 유동이 성층을 이루고 있는 것을 확인할 수 있다. θx = 0에서 수평으로 등온도면이 형성되고 있으며 θx = +50에서는 기울어진 온도분포를 보이는데 이것은 공기층이 중력에 대해서 기울어져 있기 때문이다. 또 상부에 저속구간이 발생하는 것도 확인할 수 있다. Fig. 11. (a)의 중심부에서 세로로 3차원 유동으로 온도분포가 다르게 나타나고 있는 것을 확인할 수 있다. 몇 개의 구간으로 나누어지고 있다. 이러한 유동 특성의 변화는 열전달율을 높이는 요인으로 작용한다. Fig. 11. (e)는 y방향으로 기울어진 θy = 30에서의 등온도면이다. 다른 것과 같이 성층이 되어 있지만 중력의 방향이 달라 기울어진 방향이 다른 등온도면을 보인다. θy방향으로 기울어짐에 의해 유동 방향이 차이를 보이고 있지만 방향 이외에 2차원 형태의 유동은 유지하고 있어 열전달의 변화는 거의 없는 것을 알 수 있다.
Fig. 12.는 θy에 따른 중심부에서의 유선을 나타내고 있다. 각도에 따라 중심부의 정체 구간이 많이 치우쳐진 것을 볼 수 있으나 이는 중력의 방향이 바뀌어서 정체 구간의 방향이 바뀌었기 때문이다. 10도까지는 0도와 거의 같은 현상을 보인다.
Fig. 13.은 등속도면(iso-velocity magnitude)으로 θx = 0, +50, -50일 때 확연한 차이를 보인다. 각도가 커짐에 따라 상부와 하부의 정체 구간이 넓어지고 θx = +50가 되면 가로로 누워있는 것과 비슷해진다. θx = -50인 경우는 3차원유동이 나타나며 Bernad cell과 비슷한 2차 유동이 발생한다. 상승하는 기류와 하강하는 기류는 대칭적인 유동을 가지고 있어 저온부의 하부에서 비슷한 모양을 보인다.
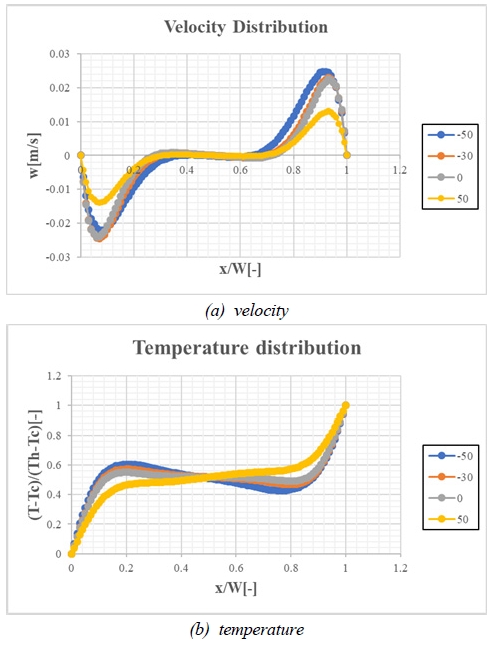
Fig. 14. 공기층 중심부(h/2, w/2)에서 x축을 따라 온도(Fig. 14. (b)), z방향 속도(Fig. 14. (a))를 각각 기울어진 각도에 따라 비교하였다. θx가 +로 증가함에 따라 상하부에 존재하는 저속구간으로 인해 벽면을 따라 흐르는 유속이 감소하고 벽면에서 열전달이 감소하게 된다. 동시에 Fig . 14. (b)에서 보듯이 온도 구배도 급격히 감소하게 된다. 모든 경우 중심부에 정체 구간이 발생하고 있지만 θx가 (-)로 증가함에 따라 줄어드는 현상을 보인다. 특히 θx = -50에서 많은 차이를 보인다. 벽면 근방에서 속도가 증가할 뿐 아니라 중심부의 정체 구간도 감소하고 있다. 이러한 속도의 변화는 온도의 기울기 차이로 나타난다.
4. 결론
건물의 외벽에 설치하는 IUES가 자연 대류 모드로 운전할 때 공기층의 각도변화에 따라 공기층의 자연 대류현상의 변화를 수치적 계산을 통하여 관찰하였다. 기울어짐이 없는 경우 고온면을 따라 공기는 부력에 의해 상승하고 저온면을 만나 하강하며 벽면 근방의 상승과 하강기류가 발생하며 중심부에 정체 구간이 생기는 전형적인 자연대류의 현상을 보인다. 양의 방향(θx)으로 기울어지는 경우, 중력방향과 상부면(혹은 하부면)이 이루는 각도 인해 “ㄱ”자 형태의 문턱이 발생하고 이에 따라 상부와 하부에 저속구간이 발생하고 기울어진 각도에 비례하여 유속이 감소하고 열전달이 줄어들었다.
반대로 음(-)으로 기울어지는 경우 양으로 기울어진 것과 같은 문턱이 존재하지 않아 -30도까지는 특별한 유속과 열전달량에 변화를 보지 않았으나 -50도 이르면서 2차 유동이 발생하고 유동특성 변화를 나타내었으며 열전달 또한 급격히 증가하였다. y축을 기준으로 기울어진 경우(θy)에는 유동의 방향이 중력으로 인해 급격하게 변하는 현상은 관찰하였으나 상대적으로 고온면과 저온면이 중력에 관하여 변화가 없어 열전달의 변화는 미미하였다. 본 연구를 통하여 IUES를 설치할 때 어느 방향으로든지 10도 이내에 설치한다면 설계 성능을 충분히 낼 수 있을 것으로 사료된다.
Acknowledgments
이 논문은 2023년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구임(20202020800030, 제로에너지건축물 구현을 위한 스마트 외장재·설비 융복합 기술개발 및 성능평가 체계 구축, 실증).
References
-
S. Sadrabadi Haghighi, H.R. Goshayeshi, M.R. Safaei, Natural convection heat transfer enhancement in new designs of plate-fin based heat sinks, International Journal of Heat and Mass Transfer, 125, 2018.10, pp.640-647.
[https://doi.org/10.1016/j.ijheatmasstransfer.2018.04.122]

-
E.M. Sparrow, A.J. Stretton, Natural convection from variously oriented cubes and from other bodies of unity aspect ratio, International Journal of Heat and Mass Transfer, 28(4), 1985.04, pp.741-752.
[https://doi.org/10.1016/0017-9310(85)90224-8]

-
D.J. Cha, S.S. Cha, Three-dimensional natural convection flow around an isothermal cube, International Communications in Heat and Mass Transfer, 20(5), 1993, pp.619-630.
[https://doi.org/10.1016/0735-1933(93)90074-6]

-
D.J. Cha, S.S. Cha, Three-dimensional natural convection flow around two interacting isothermal cubes, International Journal of Heat and Mass Transfer, 38(13), 1995.09, pp.2343-2352.
[https://doi.org/10.1016/0017-9310(94)00359-4]

-
이주희, 이용준, 전도체 주변 자연대류 현상 모사를 위한 복합열전달 수치해석 방법 개발, 한국건축친환경설비학회 논문집, 제17권 제1호, 2023.02, pp.15-27.
J.H. Lee, Y.J. Lee, Methodology of a numerical analysis method for natural convection with conjugate heat transfer, Journal of KIAEBS, 17(1), 2023.02, pp.15-27. -
김상민 외 4인, 밀폐계 내부에 존재하는 사각 배열 네 개 원형 실린더의 대각 방향 위치 변화에 의해 발생하는 3차원 자연대류 현상에 관한 연구, 대한기계학회논문집 B, 제45권 제10호, 2021.10, pp.531-540.
S. Kim et al., Study on three-dimensional natural convection induced by variation in the diagonal positions of four cylinders with a rectangular array inside an enclosure, Transactions of the KSME, B, 45(10), 2021.10, pp.531-540. [ https://doi.org/10.3795/KSME-B.2021.45.10.531 ]
-
S.V. Patankar, D.B. Spalding, A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows, International Journal of Heat and Mass Transfer, 15(10), 1972.10, pp.1787-1806.
[https://doi.org/10.1016/0017-9310(72)90054-3]

- J.H. Feriziger, M. Peric, Computational methods for fluid dynamics, 3rd ed., Berlin, Germany: Springer, 2002.
-
최석기, 김성오, Rayleigh-Benard 자연대류 유동 해석, 한국전산유체공학회지, 제13권 제3호, 2008.09, pp.62-68.
S.K. Choi, S.O. Kim, Analysis of rayleigh-bernard natural convection, The Journal of Computational Fluids Engineering, 13(3), 2008.09, pp.62-68. -
비이엘테크놀로지, ICE v1.25 사용자설명서, 2021.
BEL Technology, ICE v1.25 user manual, 2021.