An Effective Algorithm for Transmitted Solar Radiation Calculation through Window Glazing on a Clear Day
The main objective of this study is to provide an effective algorithm of the transmitted solar radiation calculation through window glazing on a clear day. This algorithm would be used in developing a computer program for fenestration system analysis and shading device design. Various simulation methods have been evaluated to figure out the most accurate and effective procedure in estimation of transmitted solar radiation on a tilted surface on a clear day.
Characteristics of simulated results of each step have been scrutinized by comparing them with measured results of the site as well as results from other simulation programs. Generally, the Duffie & Beckman’s solar calculation method introducing the HDKR anisotropic model provided the most reliable simulation results. The DOE-2 program usually provided over-estimated simulation results. The estimation of extraterrestrial solar radiation and beam normal radiation were conducted pretty accurately. However, the solar radiation either on horizontal surface or on tilted surface involves complicated factors in estimation. Even though the estimation results were close to the real measured data during summer when solar intensity is getting higher, the estimation provided more error when solar intensities were getting weaker. The convex polygon clipping algorithm with homogeneous coordinates was fastest model in calculation of sunlight to shaded area ratio. It could not be applied because of its shape limitation.
Keywords:
Solar radiation calculation, Analysis of building energy performance, Computerized building energy simulation, Energy-efficient fenestration design, Weather file, Shading analysis1. Introduction
1.1. Research Background and Objective
Because of increasing demands for high energy efficiency in construction and maintenance of buildings, accurate energy performance simulation through building envelopes has become one of the major issues in the architectural design process. Several general purpose computer-aided energy simulation programs have been developed that calculate the hourly heat gain and loss through shaded fenestration systems. However, most of these programs have not been incorporated in the actual building design process. The major reason is that there is a lack of suitable software to visualize the energy effects with proper graphical presentation methods 1). As the fenestration system is still the least efficient component of most residential and commercial buildings, an accurate and easy-to-use computer simulation program for fenestration and shading design is highly desirable. To develop this kind of program, profound and reliable evaluations should be conducted in order to scrutinize the characteristics of solar effects on the transparent surface of buildings.
1.2. The Proposed Program of the Research
The final objective of this research is to develop program for an energy-efficient fenestration system design, namely the Shaded Fenestration Designer (Fig. 1). This program will be able to calculate the thermal effect of solar radiation and shading devices on a transparent wall and visualize them with proper graphical presentation methods. However, development of this program consists of very complicated procedures which include: 1) thermal performance simulation such as solar geometry, solar radiation calculations, and the incident-angle-dependent heat transfer through multi-pane window systems; 2) window glazing and shading device design; 3) weather data modeling and processing; 4) user interface applying proper graphical presentation techniques; 5) usability tests by architectural designers in order to prove that the program is an adequate design tool showing the solar and shading effects that resulted from architectural design solutions.
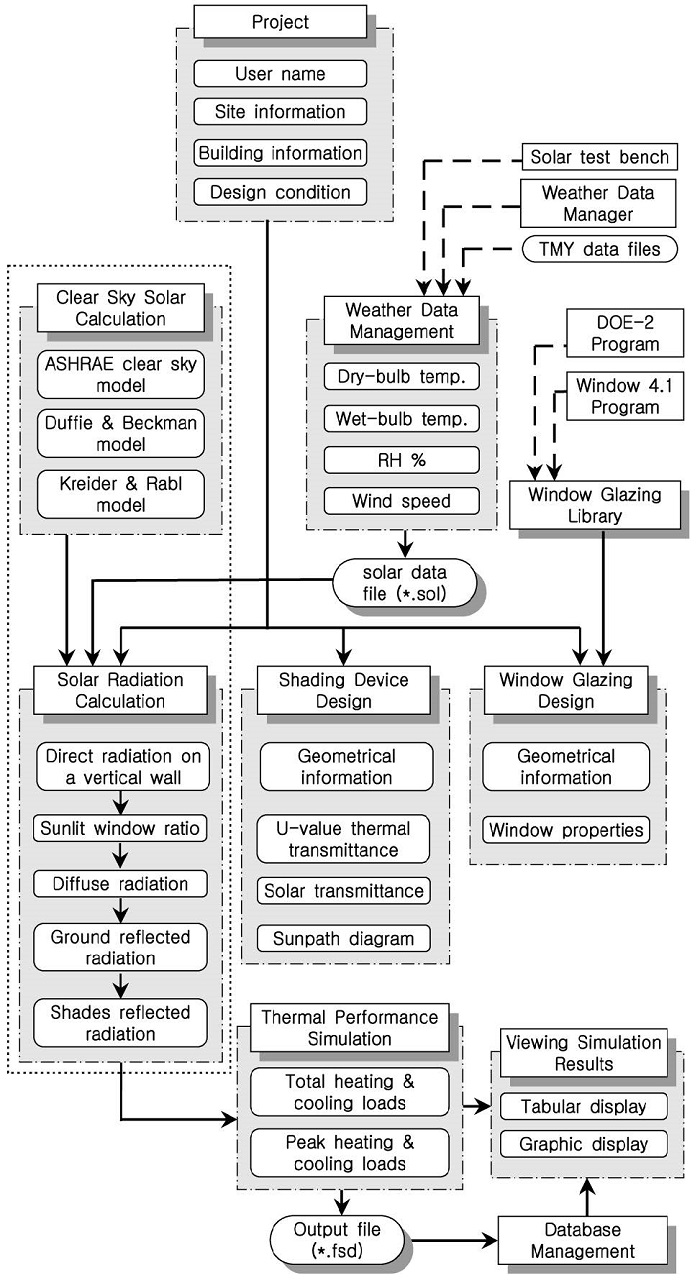
Development phases of the Shaded Fenestration Designer (SFD) program, containing the SFD Solar Data Calculator (SolrCalc) program, which is surrounded by a dotted line
As a result, the SFD program (Fig. 1) is being developed as a composite program which includes numerous subroutines and several add-in programs such as the ‘Solar Data Calculator (SolrCalc)’, the ‘Weather Data Converter (Weth-Conv)’, and the ‘Weather Data Displayer (Weth-Disp)’. Images in Fig. 2 are the screen captures of the SFD Weather Data Displayer program showing various display formats for weather data and results of building performance simulation.
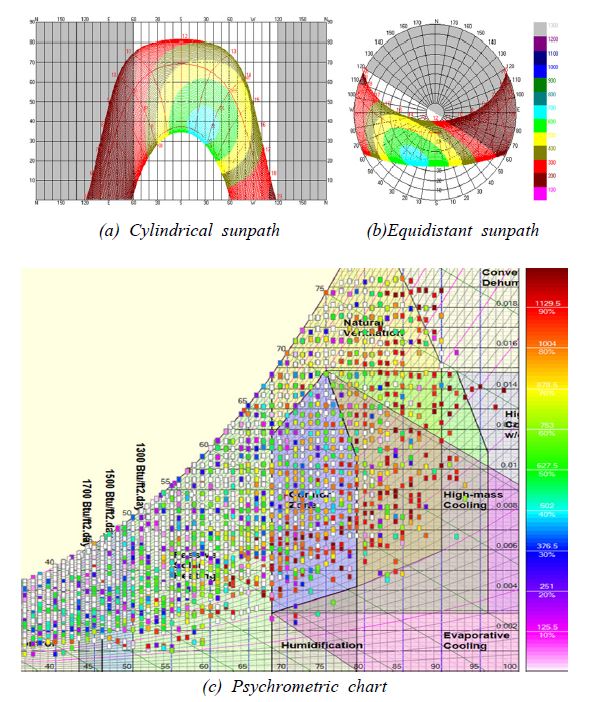
The screen image of the SFD Weather Data Displayer (WethDisp) program, displaying simulated solar radiation plotted on sunpath diagrams and measured solar radiation plotted on a psychrometric chart
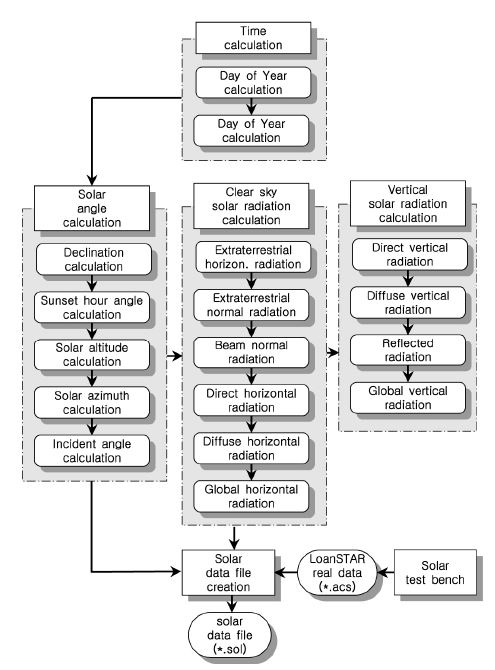
Among these subroutines, the procedures to simulate transmitted solar radiation through window glazing are the core functions in the SFD program. The SolrCalc program (Fig. 3) is an add-in program developed to satisfy this specific objective. The SolrCalc program 1) converts local civil time to local solar time, 2) calculates various solar angles related to the position of the sun for any latitude, longitude, time of day, and day of the year, 3) calculates various kinds of solar radiation on a clear day, such as extraterrestrial solar radiation, beam normal radiation, beam, diffuse, and ground-reflected solar radiation either on a horizontal surface or on a tilted surface, and 4) saves the solar data for a given period in a specific file format (*.SOL). The program provides options for the user to choose one of the solar simulation models.
1.3. Research Process and Method
As it is complicated and difficult to calculate the exact cooling load caused by transmitted solar radiation through multi-pane window glazing, we have to take into account various subtle factors and inappropriate assumptions which can cause us to make mistakes. These mistakes will increase especially when thermal resistance of the target wall is pretty high or the window area is greater than normal. Thus, the traditional heat transfer method using an analytical model, such as the CLTD/SCL/CLF method, the TFM method, or the TETD/TA method, could not be used, because these methods are difficult for an inexperienced person to manipulate and entail high possibility of error. In my previous research, the dynamic analysis method based on a finite difference model applying the HDKR anisotropic sky model and one-minute data was able to greatly reduce the number of calculation errors 2). However, this kind of mathematical analysis requires a very accurate definition of boundary conditions and a series of high level calculations. So we need a computerized easy-to-use program that could be greatly helpful to architectural designers who do not have enough knowledge of heat transfer theory that should be incorporated in their ecological architectural design process.
To process this research, equations for transmitted and absorbed solar radiation through window glazing will be analyzed and checked at every stage throughout the whole process of a computerized simulation procedure, in order to arrive at very accurate solar radiation calculation through window glazing. First, accuracy of equations for the calculation of extraterrestrial radiation and horizontal solar radiation under a clear sky will be analyzed. Then, the process of solar radiation incident on a titled surface will be verified on a comparative basis. Finally, the area ratio of the sunlit area and the shaded area will be evaluated. Widely-used computerized models for fenestration design and ways of validation and measurement of solar models also need to be reviewed.
2. Calculation of Solar Radiation under Clear Sky
Generally, simulation models for horizontal solar radiation are categorized under three headings: 1) regression models such as the Cloud-cover Radiation Model (CRM) 3), the Zhang & Huang Model (ZHM) 4), and the Saudi Arabia Model (SAM) 5), 2) mechanical models such as the Meteorological Radiation Model (MRM) 6) and the Upper –air Humidity Model (UHM) 7), and 3) models using high precision measuring instruments or satellite images 8). As regression models are required to derive regional coefficients from regressions of long-term measured weather data, it cannot be used in simulation programs using only limited site information. Even though mechanical models do not need regional coefficients, simulation process is more complicated and requires extra weather information that the usual weather station does not measure. Models using high precision measuring instruments or satellite data certainly are not suitable for the purpose of this study. Recently the author suggested a hybrid model applying the ZHM for winter season and the CRM for summer season for the sites having critical seasonal weather condition 9).
Thus, the simulation models introduced in this program are using the equations suggested by the most widely approved solar models in the United States, including those of the ASHRAE Hand Book of Fundamentals, Diffie & Beckman, and Kreider & Rabl.
2.1. Extraterrestrial Solar Radiation
The extraterrestrial solar radiation (IO,N) is the solar radiation which would be received on an earth surface if there were no atmosphere. It is quite important in terms of quantity because in many solar radiation models the estimated values of the direct and diffuse radiation on the earth’s surface are derived from it. The radiation emitted by the sun and its spatial relationship to the earth result in a nearly fixed intensity of solar radiation outside the earth’s atmosphere 10). Due to the eccentricity of the earth’s orbit, the actual value of extraterrestrial radiation varies by ±3.3%. Thus, the extraterrestrial radiation at the average earth-sun distance, i.e., the solar constant (ISQ) is used to calculate the actual intensity of the extraterrestrial radiation taking into account seasonal variations.
The ASHRAE handbook11) uses a value of 1,367 W/m2 for the solar constant. The extraterrestrial radiation varies from a maximum of 1,414 W/m2 on January 3 to a minimum of 1,323W/m2 on July 4. ASHRAE provides a table (Table 1) to determine extraterrestrial radiation for the 21st day of each month.
Duffie and Beckman 10) used a value of the solar constant rounded to 1,367 W/m2 . A simple equation with accuracy adequate for extraterrestrial radiation can be calculated by
They also provided a more accurate equation (±0.01%) developed by Spencer such as
Kreider and Rabl12) used a slightly larger value of 1,373 W/m2 for the solar constant and a value of 365.25 for the total days of the year instead of 365 used in the Duffie and Beckman model. Thus, the equation is changed to
The calculated values of extraterrestrial radiation of each month do not show much difference between these two models, and are close enough to the value of the ASHRAE Handbook. The Kreider and Rabl’s model provides about 0.5% more radiation on average than the Duffie and Beckman’s model, and the value calculated by the ASHRAE Handbook is between the former two models.
As the value of extraterrestrial radiation depends solely on the day of the year (n) and is independent of the latitude of the site, and the solar location, as well as the weather conditions, any location on the earth would have the same amount of extraterrestrial solar radiation on the same day of the year. From Table 2, we can see its peak occurs not in summer but in winter solstice (December 21) in the northern hemisphere, and the sun provides the minimum extraterrestrial radiation on summer solstice (June 21).
2.2. Clear Sky Beam Normal Radiation
The intensities of solar radiation reaching the earth’s surface vary during the year because of seasonal changes in the dust and water vapor content of the atmosphere and because of earth-sun distance changes.
In the ASHRAE method, beam normal solar radiation (IBN) on a clear day is calculated by
where A = apparent solar radiation at air mass m = 0
B = atmospheric extinction coefficient
αs = solar altitude angle (degrees)
Values of A and B are given in Table 1. These values are not the maximum value for the IB.N , but are representative of conditions on cloudless days with a relatively dry and clear atmosphere. Thus, under very clear atmospheres, IB.N can be 15% higher than the calculated value that was derived by Equation (5)11).
To develop a more accurate solar simulation model that considers the effects of altitude, visibility, zenith angle, and the four climate types of the site, both the Kreider & Rabl and the Duffie & Beckman models introduced ‘atmospheric transmittance’ for estimating the beam radiation transmitted through clear atmospheres, which had been proposed by H. C. Hottel13).
The atmospheric transmittance for beam radiation (τb) is a factor of beam normal radiation to extraterrestrial radiation (τb = IB.N/IO,N) and is determined by
where, values for α0 , α1 , and k are given in Tables 3 and 4
A = the altitude of the observer in Km
This solar transmittance for a standard atmosphere can be used for any zenith angle and altitude up to 2.5 km. For a clear sky radiation simulation, we can use the values for 23km visibility in Table 4. Table 5 shows simulated values of atmospheric transmittance for different altitudes and climate types. The simulated values ascertained that the climate type is a less critical factor in determining τb than the altitude of the site. It shows about 20% difference between the maximum and minimum values for different altitudes, but only about 5% difference for different climate types.
Table 2 shows the values of each month’s extraterrestrial radiation and normal beam radiation on clear days calculated using various solar simulation methods. The application of Hottel’s atmospheric transmittance model makes the simulation results more accurate and more flexible than the ASHRAE clear sky model. Even though the peak of extraterrestrial radiation occurs during the winter, the normal beam radiation reaches its minium value due to the minimum atmospheric transmittance of beam radiation. However, the ASHRAE clear sky model provides inaccurate results which are very different from results from other models.
The ASHRAE model itself has limited use in a computerized simulation model, because it provides only one representative value for each month. Moreover, as it does not consider the effects of altitude and visibility at the location, a great amount of discrepancy in the estimation of radiation can exist.
Bird and Hulstrom14) have also proposed a simplified clear sky model for direct and diffuse insolation on horizontal surfaces that uses three ‘rigorous radiative transfer codes’. One code is for direct normal irradiance and is called SOLTRAN 4. Two other codes, which include both the beam and the diffuse irradiance, are the BRITE Monte Carlo code and the Dave15) Spherical Harmonics code. A fairly detailed multi-layered atmosphere is constructed by defining important atmospheric parameters at each layer. Each code then uses its own algorithm to solve the radiative transfer problem. When good weather information is not available, the suggested values are given for some input parameters. Although Bird’s model might be more accurate, it is not readily applicable to a computerized model because it requires very detailed weather information such as hourly values for transmittance of aerosol scattering, transmittance of dry air absorptance, amount of ozone, aerosol optical depth, etc.
3. Clear Sky Radiation on a Horizontal Surface
Direct solar radiation on a horizontal surface for a clear day (IB,H) is determined by beam normal radiation, and the angle between the zenith and the sun. Thus,
Liu & Jordan16) developed an empirical relationship between extraterrestrial radiation and diffuse radiation for clear days. The atmospheric transmittance for diffuse radiation (τb) is the ratio of clear sky diffuse radiation to extraterrestrial radiation on a horizontal surface (τb = IB,H / IO,H) and is calculated by
From the above equations diffuse solar radiation on a horizontal surface on a clear day (IB,H) can be calculated by
Thus, total solar radiation on a horizontal surface on a clear day (IG,H) is
The Equation (10) shows that the total solar radiation on a horizontal surface under clear sky can be calculated only by extraterrestrial radiation (IO,N), zenith angle (θz), and atmospheric transmittance for beam radiation (τb). However, one can calculate the estimated clear day solar radiation on a horizontal surface if the zenith angle, altitude, and the climate type for the location are given.
Table 6 shows the simulation results of beam, diffuse, and global radiation calculated using the methods of ASHRAE, Duffie & Beckman, and Kreider & Rabl. As we can expect, the maximum radiation on a horizontal surface reaches its maximum point either in May or in June, and its minimum in December.
4. Clear Sky Radiation on a Tilted Surface
Total solar radiation incident on a tilted surface can be calculated as the sum of beam radiation, diffuse radiation from the sky, and radiation reflected from various surfaces such as the ground, external shades, and neighboring objects that block the view of the surface. If the view of the surface is blocked from direct sunlight, the total incident beam radiation on a tilted surface (IB,P) is
where Rb is the tilt factor which is the ratio of the beam radiation component on a tilted surface to that on a horizontal surface, and Fs is the sunlit factor defined by the sunlit area divided by the total surface area. When the incidence angle of direct sunlight (θi) is known,
In general, there are two kinds of solar radiation models based upon the method of simulating diffuse solar radiation: an ‘isotropic model’ and an ‘anisotropic model’. In an isotropic sky model, it is assumed that diffuse radiation is isotropic or constant. In other words, the diffuse radiation from the sky is the same regardless of the orientation. However, in an anisotropic sky model, the calculation of the diffuse radiation component on a tilted surface is a little more complicated. Diffuse radiation actually consists of three different components: the ‘isotropic diffuse’ radiation delivered uniformly from the sky hemisphere, the ‘circumsolar diffuse’ radiation scattered around the direct rays of the sun, and the ‘horizon brightening’ which is concentrated near the horizon (Fig. 4).
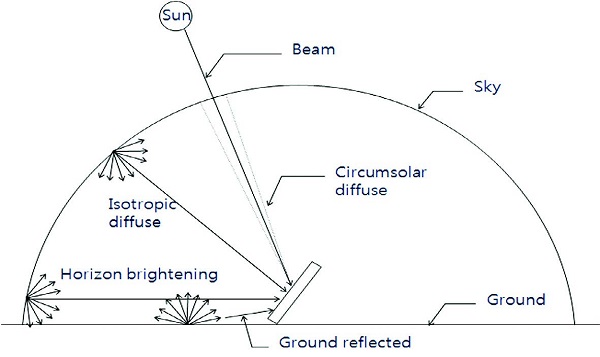
Beam, isotropic diffuse, circumsolar diffuse, horizon brightening, and ground reflected radiation on a tilted surface
The Liu and Jordan17) model for diffuse radiation is currently the most widely used. In this model, the solar radiation on a tilted surface (IG,P) is composed of the beam, the isotropic diffuse, and the ground-reflected radiation. Kreider and Rabl used the simple isotropic model, and suggested the equation for the global irradiance on a titled surface as follows:
When vertical surface and the ground in front of the surface is not shaded, the titled surface angle θp = 90o and Equation (13) becomes simply
Reindl et al.18) developed an improved anisotropic model called the ‘HDKR model’ by adding a horizon brightening component to the model originally developed by Hay and Davies19) and modified by Klucher20). This model uses an ‘anisotropy index’ to determine the transmittance of the atmosphere for beam radiation. It is assumed that isotropic diffuse radiation from the sky has the same angle as beam radiation. The diffuse radiation on a tilted surface (ID,P) using the HDKR model is calculated by
where Ai is an anisotropy index and defined by
Perez et al.21) also developed another anisotropic sky model which considers the zenith angle of the direct beam, cloud clearness, air mass, and the brightness coefficient of the sky. Diffuse radiation on a tilted surface is again calculated by
where F1 and F2 are circumsolar and horizon brightness coefficients determined by three parameters that describe the sky conditions: the zenith angle, cloud clearness, and brightness. The values of F1 and F2 are calculated from the table for brightness coefficients.
The previous study ascertained that the method developed by Liu and Jordan is less accurate than the anisotropic models22). The model developed by Perez et al. is also difficult to apply in a computer program, because it requires values that weather stations do not usually measure. Thus, the anisotropic model developed by Reindl et al. (i.e., HDKR model) is the most suitable for the calculation of diffuse radiation on a vertical surface.
The ground-reflected solar radiation on a tilted surface (IR,P) is determined by the total radiation on the horizontal surface (IG,H), the view factor of the surface to the ground (Fgrd), and the ground reflectance (ρg). For a surface directly in the front of a collector extending in all directions, the view factor to the ground is (1 - cosβ/2.
Generally, in sky radiation model the reflected radiation from the surrounding objects is ignored, because it is much smaller than the reflected radiation from the ground. However, in the case when a large portion of the window surface is blocked by external surfaces, the reflected radiation from these surfaces should be considered. The total reflected radiation from the surrounding surfaces (IR,i) can be calculated by the multiple of the solar radiation incident (Ii) on the ith surface, the diffuse reflectance(ρi) of that surface, and the view factor(Fi) from the ith surface to the analyzed tilted surface.
Finally, the total solar radiation on a tilted surface (IG,P) is calculated as the sum of these components. Thus, the total solar radiation on a tilted surface is
For the computerized algorithm of the total solar radiation incident on a tilted surface, Equation (19) was most suitable. In this equation, it is critically important to calculate the incident angles and view factors between glazing and shading objects.
Table 7 shows the simulation results tested for solar radiation on a vertical wall facing 15oSE. It clearly shows the rapid decrease of direct radiation during the summer season (e.g., the value in June 21 is just about 10 % of that in December 21 in Duffie & Beckman model), and almost constant values of diffuse radiation throughout the whole year. However, the reflected radiation increases during the summer season.
5. Calculation of Transmitted & Absorbed Radiation through Window Glazing
When the reflection and absorption losses through the glazing are considered, the transmittance (τ) of a single-glazed window can be calculated by applying ray-tracing methods to Fresnel’s equation and Snell’s equation. The total reflection (γ) of unpolarized radiation was calculated using perpendicular (γ⊥ ) and parallel (γ∥ ) components of unpolarized radiation as follows
where Ii and ir are incident and reflected solar radiation, and θ1 and θ2 are incidence and refraction angles respectively. The total transmittance (τ) of single-pane glazing can be calculated applying the ray-tracing method to Fresnel’s equations as follow
where τ⊥ and τ∥ are the perpendicular and parallel components of transmittance of the glazing and τα is the transmittance of glazing when only absorption losses have been considered. The value of τα is defined as,
where K = the extinction coefficient
L = the thickness of the glazing
The total amount of the transmitted solar radiation through window glazing can be calculated from the above equations. However, some portion of the transmitted solar radiation will be absorbed by the inside surface and some will be reflected back to the glazing. Thus, for the more accurate estimation of heat gain from the transmitted solar radiation, we need to calculate how much of the transmitted solar radiation is actually absorbed by the inside surfaces. The total solar radiation transmitted through glazing and absorbed by the inside surfaces can be calculated using the ‘transmittance-absorptance product (τα)’ as follows
Applying the same ray-tracing method here the (τα) can be calculated by
where ρd is the reflectance of the glazing for the diffuse radiation from the inside surface and α is the absorptance of the inside surface. This solar absorptance is dependent on the angle of incidence of the radiation striking the surface, and can be calculated as a function of the normal incidence for a flat black surface as follows
where αn is the normal incidence for a flat black surface and θ is the incidence angle on the surface.
Fig 5 shows the solar test bench, which was used for the validation of the transmitted solar radiation calculation as well as the glazing transmittance test. Besides this solar test bench, a physical model was constructed and used to collect the real measured transmitted solar radiation though window glazing. For more detailed description of physical model and validation of the simulation model, please refer to the previous research22).

Configuration of solar test bench (a) multi-pyranometer array with an artificial horizon, (b) Eppley normal incidence pyrheliometer, (c) horizontal solar transmittance test box, (d) shadow band, (e) Eppley shadow band pyranometer, (f) Eppley precision spectral pyranometer, (g) test stand for calibrating pyranometers
6. Calculation of Sunlight to Shaded Area Ratio
To calculate very accurately the transmitted and absorbed solar radiation through glazing, the shading analysis must be included in the computerized calculation process.
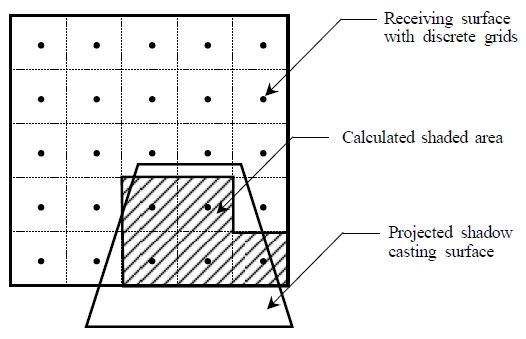
Several methods have been developed for the calculation of the sunlit and shaded area of a window. One of the simplest methods is an algorithm with ‘discrete element analysis with grids’ (Fig. 6). This method was first developed by Groth and Lokmanheim and used in the earlier version of DOE-223) and BLAST24). In this method, the receiving surface is divided into a two dimensional grid. The center point of each element is then tested by a shading projection algorithm to determine whether it is in sunlit or shaded areas. The sum of the sunlit or shaded grid elements is then used to obtain the sunlit and shaded fraction, respectively. Unfortunately, this method can require excessive processing time for higher resolution. Furthermore, it can only solve rectangular plane surfaces, which means that non-rectangular surfaces must be represented with combinations of rectangular planes.
In the recent version of DOE-2, an ‘improved bar-method’ (Fig. 7) was developed that uses bars instead of grids for a discrete element analysis. This method increased both the speed and accuracy of the calculation. However, the processing speed is still dependent on the desired accuracy and the method still has similar geometrical limitations as the grid method, although not as restrictive.
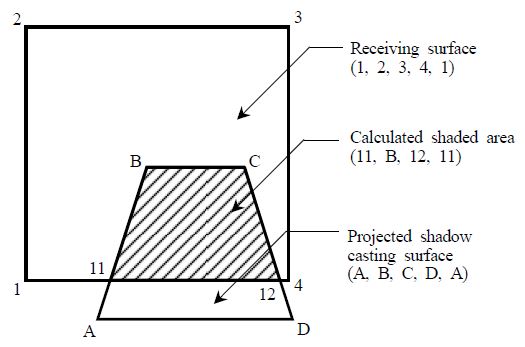
The most recent version of BLAST uses a ‘convex polygon clipping algorithm with homogeneous coordinates’ (Fig. 8) developed by Walton25). In Walton’s method, the n dimensional Cartesian coordinates are transformed into n+1 dimensional homogeneous coordinates. For example, a point given by two dimensional coordinates (x, y) is represented by three dimensional coordinates (hx , hy , h), where h is an arbitrary number. After the coordinate transformation, the algorithm finds the vertices of one polygon within the other and visa versa. Then, the intersecting points of the boundary of both polygons are determined. These overlapped vertices and intersecting points are then transformed again into Cartesian coordinates, ordered clockwise and the area is computed. Though this method is much faster than the discrete element analysis method, it is restricted to the use of convex polygons.
7. Conclusion
The extraterrestrial radiation and beam normal radiation on a clear day were estimated pretty accurately from most solar models. Even though the intensity of direct solar radiation is determined by seasonal variations and atmosphere conditions such as water vapor and dust in the air, the simulation results were pretty close to the real measured data.
The intensities of diffuse radiation either on a horizontal surface or a tilted surface were almost the same throughout the whole year. However, as the tilt factor Rb decreases rapidly during winter, the direct and reflected solar radiation also decreased in the same way. In this case ASHRAE clear sky model produces greater errors than we had expected and showed some limitations in being applied in a computer program.
The strength and incident angle of beam radiation on a transparent surface determine the intensity of transmitted and absorbed solar radiation through window glazing. When the window is partly blocked with shading devices or external walls, the estimation of transmitted solar radiation becomes more complicated, because it involves three dimensional shading analysis. Even though the convex polygon clipping method was faster than other models, it was restricted to certain shapes of the shaded area.
For the validation process in the development of the program in this research, two different types of accuracy tests were conducted (i.e., the comparative test and the empirical validation test). The comparative test was conducted by comparing the simulated results against the results of the DOE-2 program. For the empirical validation test, a specially designed physical test box was constructed and tested under various conditions. The environment of the physical model was restricted to focus on the effects of solar gain through window glazing.
A series of comparison tests of the simulation results from these models against solar data measured on the solar test bench as well as simulated results from other simulation programs demonstrated that Duffie & Beckman’s method introducing the HDKR anisotropic model has provided the most reliable simulation results. The simulation results were pretty close to the real measured data when the intensity of solar radiation was relatively high. However, as the solar intensity becomes lower in winter, the differences of estimation results produced more errors.
The main aim of this study is to devise an effective algorithm for complicated and delicate problems which can be calculated by step by step series of calculations the result of which can correct previous mistakes in our assumptions. This study shows how important experimental and theoretical validation is at each stage of the calculation process. This is especially true when dealing with complicated matters in our research such as the transmitted solar radiation through multi-pane window systems. Scrutinizing advantages and limitations of simulation models at each stage could improve the mathematical precision and practical usability of the computer program appling the algorithm that we had proposed.
References
- Kei-Whan Oh, Development of psychrometric chart program applying animated graphical method for effective visualization of weather & building performance data, Journal of KIAEBS, (2014, Jun), 8(3), p117-126.
- Kei-Whan Oh, A study on the dynamic numerical analysis for the solar radiative cooling loads–focused on the experimental research using the finite difference model, Journal of the Regional Association of Architectural Institute of Korea, (2006, Sep), 8(3), p91-100.
-
F Kasten, G Czeplak, Solar and terrestrial radiation dependent on the amount and type of cloud, Solar Energy, (1980), 24, p177-189.
[https://doi.org/10.1016/0038-092X(80)90391-6]
- Q.Y Zhang, Y.J Huang, Development of typical year weather files for Chinese locations, ASHRAE Transactions, (2002), 108(2), p1063-1075.
- A Akram, , Simulation and modeling of solar radiation in Saudi Arabia, Renewable Energy, (1995), 6(2), p107-118.
- V Badescu, Modeling solar radiation at the earth’s surface, Chapter 14, The meteorological radiation model (MRM): Achievements and Applications, (2008).
- K Yang, T Koike, Estimating surface solar radiation from upper-humidity, Solar Energy, (2002), 77(2), p177-186.
- R Perez, , A new operational model for satellite-derived irradiances: description and validation, Solar Energy, (2002), 73(5), p307-317.
- K.H Kim, J.K Oh, Impact by estimation error of hourly horizontal global solar radiation models on building energy performance analysis, KIEAE Journal, (2014, Apr), 14(2), p3-19.
-
J Duffie, W Beckman, Solar Engineering of Thermal Processes, John Wiley & Sons, Inc, (2006).
[https://doi.org/10.1002/9781118671603]
- ASHRAE, Handbook of Fundamentals, American Society of Heating, Refrigerating and Air-Conditioning Engineers, (2005).
- J.F Kreider, A Rabl, Heating and Cooling of Buildings, McGraw-Hill, Inc, (1994).
- H.C Hottel, A simple model for estimating the transmissivity of direct solar radiation through clear atmosphere, Solar Energy, (1976), 18, p129.
- R. E Bird, R. L Hulstrom, A simplified clear sky model for direct and diffuse insolation on horizontal surfaces, SERI/TR-642-761, Solar Energy Research Institute, (1981).
-
J. V Dave, Extensive datasets of the diffuse radiation in realistic atmospheric models with aerosols and common absorbing gases, Solar Energy, (1978), 21, p361-369.
[https://doi.org/10.1016/0038-092X(78)90167-6]
- B. Y Liu, R. C Jordan, The interrelationship and characteristic distribution of direct, diffuse and total solar radiation, Solar Energy, (1960), 4(3), p1.
- B. Y Liu, R. C Jordan, The long-term average performance of flat-plate solar energy collectors, Solar Energy, (1963), 7(2), p53-74.
- D.T Reindl, W.A Beckman, J.A Duffie, Evaluation of hourly tilted surface radiation model, Solar Energy, (1990), 45, p9-17.
- J. E Hay, J. A Davies, Calculation of the solar radiation incident on an inclined surface, Proceedings First Canadian Solar Radiation Data Workshop, Ministry of Supply and Services, Canada, (1980), 59.
- T. M Klucher, Evaluating model to predict insolation on tilted surfaces, Solar Energy, (1979), 23, p111-114.
- R Perez, R Stewart, R Seals, T Guertin, The Development and Verification of the Perez Diffuse Radiation Model, Sandria National Laboratories Contractor Report, SAND 88-7030, (1988, October).
- J. K Oh, Development and Validation of a Computer Model for Energy-efficient Shaded Fenestration Design, Ph.D, Dissertation, Texas A&M University, (2000).
- LBL, DOE-2 Engineers Manual Version 2.1A, Lawrence Berkeley Laboratory and Los Alamos National Laboratory, LBL-11353 Rev.2, (1982).
- BSO, BLAST User Reference, Blast Support Office, University of Illinois at Urbana-Champaign, (1993).
- G. N Walton, The application of homogeneous coordinates to shadowing calculations, ASHRAE Transactions, (1979), 85(1), p174-180.