클러스터링 기반의 인공신경망을 이용한 건축물 가스에너지소비량 예측 및 평가
@ 2018 KIEAE Journal
Abstract
Prediction of building energy consumption is an important indicator of effective energy use and savings. Accordingly, studies are actively carried out to find energy use patterns in buildings or to predict energy consumption, especially machine learning technique have been successfully applied in analyzing building energy consumption data. In this paper, we propose a clustering method based on the dynamic time warping(DTW) algorithm, and applied to Artificial neural network(ANN) prediction model to improve the prediction accuracy of gas energy consumption in buildings.
To establish cluster-based ANN prediction model, monthly gas energy consumption data of buildings provided by the Korean government were collected. Using the collected data, this study analyzed representative patterns of gas energy consumption through DTW clustering method, and built an ANN prediction model based on these patterns. In addition, the accuracy of the DTW clustering-based ANN predictive model was compared with the general model to confirm whether the accuracy of the predictive model would be improved.
It was confirmed that cluster-based ANN prediction model showing representative pattern was analyzed about 12.7% more accurate than general model.
Keywords:
Building energy prediction, Artificial neural network, Dynamic time warping, Hierarchical clustering키워드:
건물 에너지 예측, 인공신경망, 동적 타임 워핑, 계층 클러스터링1. 서론
1.1. 연구의 배경 및 목적
인구의 증가, 건물 및 기술 분야의 급속한 발전은 에너지소비량을 증가시키고 있다. 따라서 건물의 에너지소비 예측은 효과적인 에너지 사용 및 절약의 중요한 지표가 된다. 뿐만 아니라, 건물 에너지 수요예측은 설비 구축 및 장기적 수급계획, 소비 효율구간 탐색 등 기관 또는 사회적 비용을 최소화 할 수 있는 근거가 될 수 있다[1]. 이에 따라 건물의 에너지 및 부하에 대한 사용 패턴을 찾거나, 에너지소비량 예측에 관한 연구가 활발히 진행되고 있다. 특히 최근에는 빅 데이터(Big data)를 기반한 기계학습(Machine learning) 모델을 활용하여 건물 에너지소비 패턴분석 및 예측 분야에서 인공지능(Artificial Intelligence; AI)을 실현하고 있다.
여러 기계학습 모델 중에서도 인공신경망(Artificial Neural Network; ANN)은 자료를 구성하는 법칙을 학습하는 데 중점을 두어 시계열 자료의 분석 및 예측에 효과적인 것으로 알려져 있기 때문에, 최근 건물 에너지 분야에서 많이 쓰이고 있다[2].
인공신경망을 활용한 건물에너지 분야의 연구로, Kang은 인공신경망을 활용하여 VRF(Variable Refrigerant Flow)시스템의 에너지성능 향상을 위해 냉방에너지 사용량을 예측하였으며[3] Park은 냉방에너지소비를 최소화하는 것을 목적으로 다양한 셋백온도에 따른 냉방부하를 예측하는 인공신경망모델을 제안하였다[4]. 또한 Li는 ANN, Hybrid neuro-fuzzy 등을 활용하여 건물에너지소비량을 예측하였고[5], Neto의 연구에서는 ANN의 예측결과와 건물에너지 예측 시뮬레이션 결과를 비교 분석하여 ANN 예측이 시뮬레이션 결과보다 좋은 것을 확인하였다[6].
인공신경망은 많은 자료를 학습하는 방식으로 데이터를 예측하기 때문에 회귀모델 같은 통계적 모델에 비해 예측 정확도가 뛰어난 것으로 여러 연구에서 확인되었다. 하지만 신경망 예측일지라도 대용량이며 다차원적인 데이터 집합이나 내부적 구조가 매우 복잡한 데이터 집합은 정확도가 감소할 수 있다. 이에 따라 복잡한 차원의 신경망 예측모형을 고도화하기 위한 일환으로, 여러 데이터마이닝 기법을 결합하여 예측의 정확성을 향상시키려는 연구가 시도되고 있다.
특히 클러스터링(Clustering)분석을 기반으로 인공신경망 예측모형을 구축하면 그렇지 않은 모형보다 더 높은 정확도를 나타내는 것으로 확인되었다[7]. 여기서 클러스터링(Clustering)은 적절한 기준에 대하여 동일한 군집에 속하는 데이터들을 서로 유사한 여러 개의 부분집합으로 할당하여 분류하는 기계학습의 기법으로[8], 건물의 에너지소비패턴을 정의하거나 특성을 파악할 수 있으며 이를 기반으로 구축된 예측모형은 정확도가 향상되는 것으로 확인되었다. 대표적으로, Yang의 연구에서 클러스터링을 기반으로 건물 에너지사용패턴에 따른 서포트벡터(Support vector) 예측모형을 구축하여 기존의 모형보다 향상된 정확성을 확인하였다[9].
선행연구에서 검증된 바와 같이, 건물의 에너지소비패턴이 다양함에 따라 클러스터 분석을 기초로 한 예측모형의 정확도는 기존의 모형보다 향상될 것으로 사료된다. 그러나 인공신경망을 활용한 건물에너지소비 예측과 관련된 연구 분야에서 클러스터링을 기반으로 예측모형을 구축하고, 정확도를 검증 및 평가한 연구는 부족한 실정이다.
이에 본 연구에서는 용도, 규모, 위치 등이 다양한 건물의 가스(LNG)에너지소비량 정보를 바탕으로 동적 타임 워핑(Dynamic Time Warping; DTW)기반 계층 클러스터링 분석을 실시하여 건물의 가스에너지소비 패턴을 확인하였다. 클러스터링 분석을 통해 도출된 가스에너지소비 패턴을 기반으로 인공신경망 예측모형을 구축하여 정확도를 평가하였으며, 예측모형의 예측성능을 향상시키고자 하였다. 에너지소비 예측성능의 향상은 건물에너지의 관리측면에서 보다 효율적인 공급 및 수요관리가 가능할 것으로 사료된다.
1.2. 연구의 방법 및 범위
본 연구에서는 건물 가스에너지소비량 예측모형을 구축하기 위해 다양한 규모, 용도, 지역의 건물에 대한 월별 가스사용량을 수집하였다. 동적 타임 워핑(Dynamic Time Warping; DTW)거리 기반 계층 클러스터링 기법을 활용하여 수집된 가스에너지소비량의 패턴을 확인하였으며, 이를 기반으로 인공신경망(Artificial neural network; ANN) 예측을 실시하였다. 또한, 클러스터링 전과 후의 인공신경망 예측 성능을 비교 평가함으로써 기존의 인공신경망 예측모형의 고도화 방안을 제시하였다.
클러스터링 및 인공신경망의 구현은 공개 데이터분석 소프트웨어인 R을 이용하였다.
2. 클러스터링 및 인공신경망의 개념과 이론
2.1. 동적 타임 워핑(Dynamic Time Warping; DTW) 거리 기반 계층 클러스터링
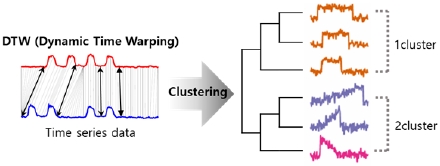
본 연구에서는 시계열 데이터 형태인 건물 가스에너지소비량의 패턴을 도출하기 위해 동적 타임 워핑(Dynamic Time Warping; DTW)거리 기반의 계층 클러스터링 기법을 사용하였다.
여기서 동적 타임 워핑(DTW)이란 시간 차원에서 비선형적으로 변화하는 두 데이터의 유사성을 측정하기 위한 알고리즘으로, 시계열 간의 사상(mapping) 상관을 찾아내어 짝을 이루는 관측치 간의 특정한 거리 (Xai, Ybi)를 최소화할 수 있도록 고안된 방법이다[10]. 동적 타임 워핑에서 관측치 간의 거리 정의는 (식1)과 같다.
| (식1) |
동적 타임 워핑 거리 기반 계층 클러스터링 기법은 위에서 설명한 DTW 거리 정보를 토대로, 단계적으로 계층적인 그룹을 형성하여 많은 수의 데이터를 유사 거리정보에 따라 분류하는 기법이다.
이 때, 적정 개수의 군집 수를 설정하여 유사한 데이터들이 같은 군집에 구성되게 해야 하며, 군집이 너무 많거나 적으면 데이터의 분류 특징을 정확이 파악할 수 없다. 따라서 본 연구에서는 군집의 개수를 설정하는 방법으로 Kanti Mardia(1979)가 제안한 (식2)를 사용하였다[11]. 여기서, n은 데이터의 개수를 뜻한다.
| (식2) |
다음 Fig. 1.은 동적 타임 워핑 거리기반 계층 클러스터링에 대한 다이어그램을 나타낸다.
2.2. 인공신경망(Artificial neural network; ANN)
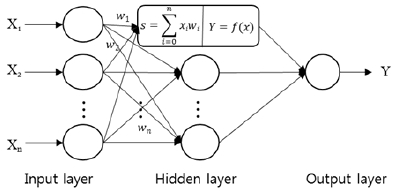
인공신경망(Artificial neural network ; ANN)은 인간의 신경세포 뉴런(neuron)과 뉴런을 연결하는 시냅스(synaps)의 관계를 수학적으로 모델링한 알고리즘이다. 상호 연결된 뉴런은 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)으로 구성되며, 뉴런들 사이는 가중치(weight)의 강도로 상호 연결되어 있다. 신경망 뉴런의 처리과정은 (식3)과 같으며, xi가 뉴런의 입력일 때 wij는 입력층의 i번째 뉴런과 j번째 뉴런 사이의 가중치(weight)로 지식을 축적한다[1]. 축적된 가중치 합은 활성화 함수(Activation function)에 의해 0~1사이 값으로 변환하여 출력하며, 본 연구에서는 (식4)의 시그모이드(sigmoid)함수를 사용하였다. 이러한 인공신경망의 구조 및 개념은 Fig. 2.와 같이 나타낼 수 있다.
| (식3) |
| (식4) |
인공신경망은 통계적 수식에 의존하지 않고 주어진 자료를 표현하는 일종의 규칙을 찾아내므로 비선형성을 가진 시계열 자료를 예측하는 데에 유리한 것으로 알려졌다. 이와 같은 특성 때문에 인공지능 분야를 비롯한 문자인식, 화상처리, 자연언어 처리, 음성인식 등 다양한 분야에서 이용되고 있다[12].
3. 클러스터링을 이용한 가스에너지소비량 패턴분석
3.1. 가스에너지소비량 패턴분석 개요
본 연구에서는 건축물의 가스에너지소비량 패턴을 분석하고 예측모델을 구축하기 위하여, 국토교통부에서 제공하는 건물에너지 정보공개시스템을 통해 권역별 지역의 가스에너지소비량 정보를 지번별로 수집하였다. 또한, 건축물의 용도, 면적, 승인년도 등의 건축물 정보는 건축행정시스템 세움터 사이트를 통해 추가 수집하였다. 이에 따라 수집된 데이터는 총 921개 지번별 가스소비량 및 건축물정보이며 제공되는 자료 형태가 월별 가스소비량 값으로, 본 연구에서는 2012년~2016년의 1월~12월 데이터를 활용하였다.
한편, 가스에너지소비량의 패턴분석 시 건물 규모에 따른 영향을 배제하여, 에너지소비패턴에 따른 클러스터링의 결과가 명확할 수 있도록 데이터를 정규화 처리하였다. 정규화 처리 방법에는 최소최대 기법을 이용하였으며, (식5)에 의해 가스에너지소비량 데이터를 0~1 사이 값으로 변환하였다.
| (식5) |
수집 및 변환된 데이터를 이용하여 동적 타임 워핑 거리 기반 계층 클러스터링 분석을 실시하였으며, 데이터 분류 묶음인 군집의 개수는 (식 2)에 의해 21개로 설정 하였다.
3.2. 가스에너지소비량 클러스터링 패턴 분석
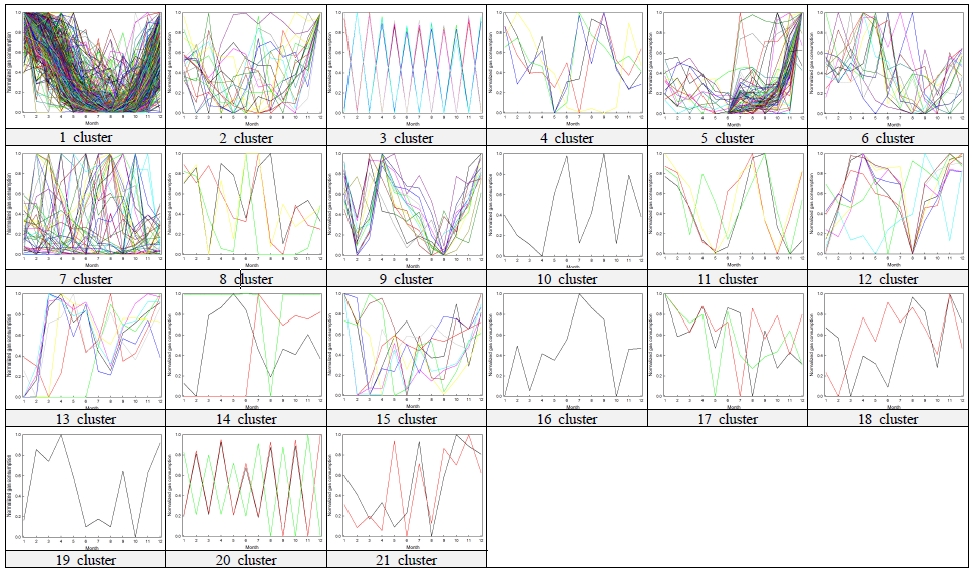
DTW 거리기반의 계층 클러스터 방법론에 의해 가스에너지소비량을 분석한 결과, Fig. 3.과 Table 1.의 결과를 나타내었다.
Table 1.에서 cluster 1~21은 클러스터링 분석 결과 형성된 각각의 군집을 나타내며, Cluster size는 각 군집에 분류된 건물의 개수를 의미한다. 또한, Average distance는 DTW 거리 계산법에 의한 각 군집의 거리 중심개체(center case)와 나머지 개체(case) 간의 평균 거리를 의미한다. 이 때, Cluster size가 크고 Average distance가 작은 경향성을 보일수록 유사패턴의 데이터가 Grouping 되었다고 할 수 있다. 반면 Cluster size가 작거나 Average distance가 큰 경우 대표 군집에서 탈락한 아웃라이어(Outlier)데이터로 판단할 수 있다.
클러스터링 분석 결과, 1 cluster에 가장 많은 건물 개체가 분류되었으며 그 다음으로 5 cluster, 7cluster인 것으로 분석되었다. 1 cluster에는 전체 데이터 case 중 74.8%인 689개의 건물 가스에너지 사용패턴이 분류되어, 연간 건물 가스에너지소비의 대표 패턴인 것으로 판단된다. 1 cluster의 가스소비량 패턴은 9월 이후 점차 증가하여 겨울철인 12월~2월은 높고, 여름철인 7~9월은 낮은 것으로 분석되었다. 이와 같은 가스에너지소비 패턴을 보인 것은 겨울철 난방부하로 인한 보일러사용에 따른 가스소비량 증가에 의한 현상인 것으로 사료된다.
그 다음으로 큰 Cluster size를 보인 군집은 5 cluster와 7 cluster로 나타났으며, 각각 76개(8.3%), 44개(4.8%)의 건물 가스사용패턴이 분류되었다. 5 cluster에는 1~5월의 데이터가 결측되어 6월 이후의 데이터만 있는 case와 1~5월 사이의 가스소비량이 비교적 낮고 6~12월에 높은 case가 분류되었다. 7 cluster은 연중 가스소비량의 변화가 적거나, 여름철인 6~9월의 가스소비량이 겨울철에 비해 높은 case가 분류된 것으로 확인되었다.
한편, 나머지 Cluster들은 Cluster size가 20개 미만이며, 분류된 case의 비율이 전체 데이터 비율의 약 2.5% 미만인 것으로 확인되었다. 따라서 1 cluster, 5 cluster, 7 cluster를 제외한 나머지 cluster에 해당하는 case는 특이 값이나 이상 값이 분류된 것으로 판단된다.
따라서 Cluster size가 컸던 3개 군집을 기반으로 인공신경망 예측모형을 구축하여 정확도를 평가하고, 클러스터링을 적용하지 않은 예측모형과의 비교를 통해 예측모형의 성능향상 정도를 확인하였다.
4. 클러스터링 기반 인공신경망 예측 및 평가
4.1. 클러스터링 기반 인공신경망 예측모델 구축
클러스터링 분석에 기반한 인공신경망 예측모델에 대한 예측성능을 평가하기 위해, 클러스터링 분석을 하지 않은 인공신경망 예측모델과 클러스터링 분석을 통해 도출된 3개 군집의 인공신경망 예측모델을 구축하였다.
신경망의 학습 정보는 역전파 알고리즘(Backpropagation)에 의해 처리하였으며, 활성화 함수는 시그모이드(sigmoid)함수를 사용하였다. 신경망의 학습률과 학습 정지 기준은 각각 0.1과 0.01로 설정하였다.
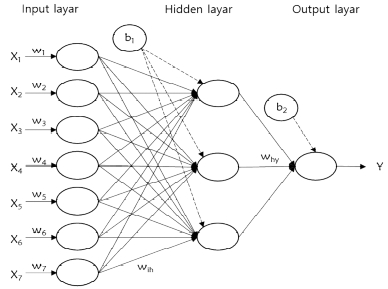
신경망의 입력층은 예측 변수 개수에 따라 7개의 뉴런으로 구성하였으며 0~1사이 값으로 정규화된 변수 값을 입력하였다. 입력된 예측변수는 Table 2.와 같다.
은닉층의 뉴런 개수는 적을 경우 네트워크의 오류 정밀도가 감소할 수 있으며, 많을 경우 네트워크 훈련시간이 불필요하게 길어질 수 있다[13]. 이에 따라 은닉층의 적정 뉴런 개수를 결정해야 하며, 본 연구에서는 Li&Yu(1995)의 연구에서 제시된 뉴런 개수 결정 식(식6)에 의해 3개 뉴런으로 구성하였다. 여기서 Nh은 은닉층의 뉴런 개수이며 n은 입력층에 입력되는 변수의 개수를 의미한다. 출력층은 목표변수인 가스에너지소비 예측 값(y)을 출력하는 1개의 뉴런으로 구성하였다. Fig. 4.는 본 연구에서 구축한 인공신경망 모델의 신경망 구조를 나타낸다.
| (식6) |
한편, 예측모델 구축 시 전체 데이터를 Train set과 Test set으로 분리해야 한다. 여기서 Train set은 예측모델을 구축할 때 사용하는 데이터를 뜻하며, Test set은 구축한 예측모델의 성능을 검증하는 데이터를 뜻한다. 본 연구에서는 Holdout method에 의해 전체 데이터의 2/3을 Train set으로, 나머지 1/3을 Test set으로 사용하였다.
위와 같은 방법론을 기초로, 수집된 모든 데이터를 활용한 기본 예측모델과 클러스터 분석을 기반한 1 cluster 예측모델, 5 cluster 예측모델 7cluster 예측모델을 각각 구축하여 예측결과에 대한 정확도를 비교 검증하였다.
4.2. 가스에너지소비량 예측 및 평가
앞서 구축한 기본 인공신경망 예측모델과 클러스터링을 기초한 세 개의 인공신경망 예측모델의 정확도를 비교 분석하고, 클러스터링 기법 적용에 따른 신경망 예측모델의 정확도 향상 정도를 평가하였다. 정확도는 실제 측정된 가스에너지소비량과 예측된 가스에너지소비량 사이의 상관관계를 확인하여 평가하였으며, 평가지표로 두 값의 회귀 기울기 및 R2, 피어슨 상관계수(Pearson correlation coefficient)를 사용하였다. 여기서 회귀 기울기와 피어슨 상관계수는 두 변수간의 선형적 관계를 판단하는 지표로, 양의 상관성이 클수록 1, 음의 상관성이 클수록 –1, 상관성이 없으면 0에 가까운 계수 값을 가진다. 따라서 회귀 기울기 및 상관계수가 0.7이상일 때 강한 상관성을 나타내어 예측성능이 뛰어나다고 판단할 수 있으며, 0.3이하일 때 낮은 상관성을 보이므로 예측정확도가 낮은 것으로 판단할 수 있다.
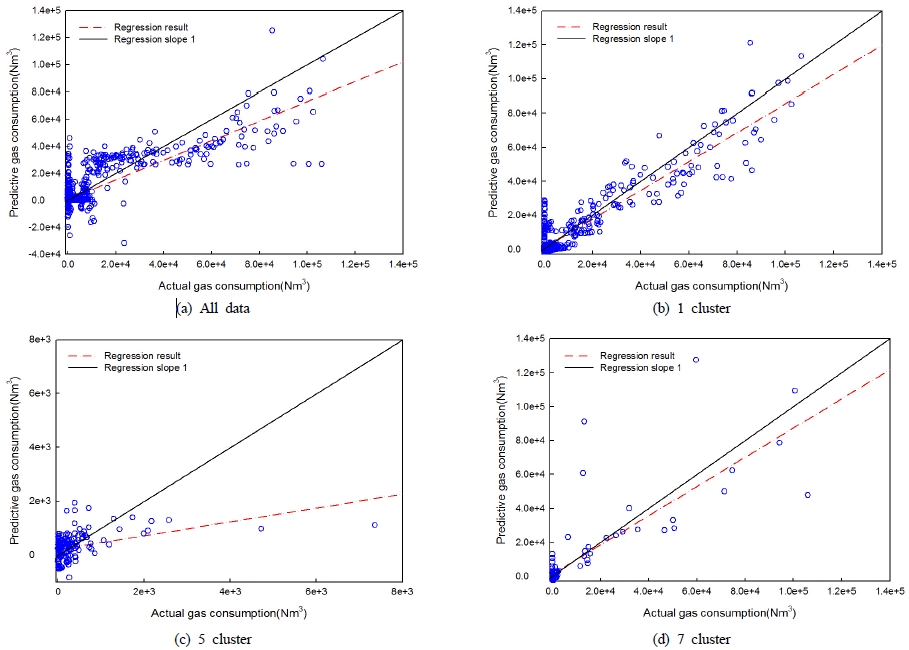
기본 예측모델과 클러스터링을 기초로 한 예측모델의 예측성능은 Table 3.과 Fig. 5.와 같이 분석되었다. Table 3.은 예측 값과 실제 값의 회귀선 기울기 및 R2와 피어슨 상관계수를 나타내며, Fig. 5.는 예측 값과 실제 값 및 회귀 그래프를 나타낸다.
클러스터링 기법을 적용하지 않은 기본 인공신경망 예측모형의 예측결과, 실제 값과 예측 값의 회귀 기울기는 0.723으로 높은 상관성을 나타냈다. 회귀 모델의 적합도를 나타내는 R2는 0.739로 비교적 높게 분석되어 인공신경망의 예측성능이 좋은 것으로 확인되었다. 또한, 두 값의 상관관계를 나타내는 피어슨 상관계수는 0.860으로 분석되어 예측 값과 실제 값 사이의 상관성이 높은 것으로 나타났다.
한편, 연간 가스에너지소비량의 대표 패턴을 보인 1 cluster의 데이터를 기반으로 구축한 예측모형의 예측결과, 회귀 기울기와 R2 이 0.85, 0.895로 분석되어 기본 예측모델에 비해 약 12.7% 더 높은 상관성을 나타냈다. 피어슨 상관계수 또한 0.946으로 분석되어 가스 에너지소비량을 매우 상관성 높게 예측하는 것으로 분석되었다.
7 cluster 기반 예측 결과의 회귀 기울기와 상관계수는 0.861과0.814로 실제 값과 높은 상관성을 가지는 것으로 분석되었다. 하지만, 회귀모형의 타당성을 나타내는 R2는 0.663으로 비교적 낮게 나타났으며, 피어슨 상관계수도 기본 예측모델보다 약 0.046 낮은 것으로 분석되었다. 이는 7 cluster의 군집크기가 전체 데이터 대비 약 4.8%로, 1 cluster나 기본 예측모델에 비해 데이터가 충분하지 못했기 때문으로 판단된다.
예측 성능이 비교적 뛰어났던 1 cluster, 7 cluster와 달리, 5 cluster의 예측모델의 예측 회귀선 및 R2은 0.257, 0.170으로 분석되었으며, 피어슨 상관계수는 0.412로 모든 지표에서 매우 낮은 상관성을 나타냈다. 인공신경망 예측은 다량의 데이터를 통해 정보학습을 이루어야 하는데, 5 cluster의 군집 크기는 전체 데이터 대비 약 8.3%로 크지 않았으며, 5 cluster에 주로 1~5월의 가스소비량이 결측된 Case가 주로 분류되었기 때문에 1~5월 정보를 적절하게 학습하지 못한 것으로 판단된다. 따라서 신경망 학습 데이터 및 정보의 부족으로 인해 예측 정확도가 매우 낮게 분석된 것으로 사료된다.
5. 결론
본 연구에서는 건물 가스에너지소비량 예측모형의 정확도 향상을 위하여, 클러스터링 분석 기반의 가스에너지소비량 패턴에 따른 인공신경망 예측모델을 구축하였다. 또한 예측결과에 대한 정확도를 확인하여 클러스터링 적용에 따른 예측성능 변화를 확인하였으며, 주요 결과는 다음과 같이 분석되었다.
클러스터링 기법 적용에 따른 인공신경망 예측모델의 정확도를 확인한 결과, 군집 크기가 가장 큰 가스에너지사용량 대표 패턴의 예측모델은 클러스터링을 적용하지 않은 신경망 예측모델보다 더 높은 정확도를 나타내는 것으로 확인되었다.
구체적으로, 가스사용량 대표 패턴으로 분류된 1 cluster를 기반으로 한 예측모델의 회귀 기울기 및 피어슨 상관 계수는 0.85, 0.946으로 분석되어, 실제 값과 매우 높은 상관성을 나타내는 것으로 분석되었다. 또한, 클러스터링을 적용하지 않은 기본 예측모델보다 회귀선 기울기 기준 약 12.7% 높은 상관성을 나타내므로, 클러스터링 기법 적용이 인공신경망 예측모델 정확도 향상에 기여하는 것으로 확인되었다.
이는, 클러스터링 분석 과정에서 에너지소비 이상 패턴을 분류함으로써 인공신경망 학습에 사용된 데이터 품질이 좋아짐에 따라 정확도 높은 예측모델이 구축된 것으로 판단된다.
한편, 5 cluster에는 대부분 1~5월 가스소비량 값이 누락된 Case가 분류되었으며, 누락된 데이터에 의한 신경망 학습으로 인해 예측모형의 성능이 감소한 것으로 사료된다. 이에 따라, 높은 정확도를 나타냈던 1 cluster, 7cluster 기반의 예측모델과 달리, 5 cluster 예측모델은 회귀 기울기 및 피어슨 상관 계수가 0.26, 0.412로 매우 낮은 예측성능을 나타내었다.
따라서 양질의 데이터가 확보된 경우, 시계열에 따른 패턴을 분류하여 예측모델을 구축하면 예측성능을 향상시킬 수 있는 것으로 확인되었다. 다만, 일, 시간과 같은 단기간 시계열에 대한 패턴은 연간 패턴에 비해 시계열 특징이 뚜렷할 것으로 예상됨에 따라 향후 연구에서 단기간 에너지소비패턴에 대한 추가 분석이 필요할 것으로 사료된다.
Acknowledgments
본 연구는 국토교통부 국토교통기술촉진연구사업의 연구비지원(18CTAP-C130211-02)에 의해 수행되었습니다.
Reference
-
문지훈, 전상훈, 박진웅, 최영환, 항인중, 인공 신경망과 지지 벡터 회귀분석을 이용한 대학 캠퍼스 건물의 전력 사용량 예측 기법, 한국, 정보처리학회논문지, 5(10), (2016), p293-302.Moon, Ji-Hoon, Jun, Sang-Hoon, Park, Jin-Woong, Choi, Yong-Hwan, Hwang, Een-Jun, An Electric Load Forecasting Scheme for University Campus Buildings Using Artificial Neural Network and Support Vector Regression, Korea, Korea Information Processing Society, 5(10), p293-302.
[
https://doi.org/10.3745/ktccs.2016.5.10.293
]

- 이예지, 데이터마이닝을 이용한 태양광발전시스템 모듈온도 예측에 관한 연구, 한국, 인천대학교 석사학위논문, (2017), p29.Lee, Ye-Ji, Prediction of Module Temperature for Photovoltaic System using Data Mining, Korea, Incheon University, (2017), p29.
-
강인성, 양영권, 이효은, 박진철, 문진우, 건물 냉방시스템의 예측제어를 위한 인공신경망 모델 개발, 한국, 한국생태환경건축학회 논문집, 17(5), (2017), p69-76.Kang, In-Sung, Yang, Young-Kwon, Lee, Hyo-Eun, Park, Jin-Chul, Moon, Jin-Woo, Development of an Artificial Neural Network Model for a Predictive Control of Cooling Systems, Korea, The International Journal of The Korea Institute of Ecological Architecture and Environment, 17(5), (2017), p69-76.
[
https://doi.org/10.12813/kieae.2017.17.5.069
]

-
박보랑, 최은지, 문진우, 셋백기간 중 건물 냉방시스템 부하 예측을 위한 인공신경망모델 성능 평가, 한국, 한국생태환경건축학회 논문집, 17(4), (2017), p83-88.Park, Bo Rang, Choi, Eunji, Moon, Jin Woo, Performance tests on the ANN model prediction accuracy for cooling load of buildings during the setback period, Korea, The International Journal of The Korea Institute of Ecological Architecture and Environment, 17(4), (2017), p83-88.
[
https://doi.org/10.12813/kieae.2017.17.4.083
]

-
Li, Kangji, Su, Hongye, Chu, Jian, Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system: A comparative study, China, Energy and Buildings, 43, (2011), p2893-2899.
[https://doi.org/10.1016/j.enbuild.2011.07.010]

-
Neto, Alberto Hernandez, Fiorelli, Fla´ vio Augusto Sanzovo, Comparison between detailed model simulation and artificial neural network for forecasting building energy consumption, Brazil, Energy and Buildings, 40, (2008), p2169-2176.
[https://doi.org/10.1016/j.enbuild.2008.06.013]

- 김용신, 클러스터별 인공 신경망 구축을 통한 데이터마이닝 모델의 성능 향상, 한국, 아주대학교 석사학위논문, (2003).Kim, Yong-Shin, Performance Improvement of a Data Mining Model by Building Artificial Nerual Networks for Individual Clusters, Korea, Ajou University, (2003).
-
윤영란, 신상헌, 문현준, 클러스터링 기반 건물 용도별 에너지 소비 패턴 분석, 한국, 한국생활환경학회지, 24(2), (2017), p232-237.Yoon, Yougn-Ran, Shin, Sang-Heon, Moon, Hyeun-Jun, Analysis of Building Energy Consumption Patterns according to Building Types Using Clustering Methods, Korea, Journal of The Korean Society of Living Environmental System, Korea, 24(2), (2017), p232-237.
[
https://doi.org/10.21086/ksles.2017.04.24.2.232
]

-
Yang, Junjing, Ning, Chao, Deb, Chirag, Zhang, Fan, Cheong, David, Lee, Siew Eang, Sekhar, Chandra, Tham, Kwok Wai, k-Shape clustering algorithm for building energy usage patterns analysis and forecasting model accuracy improvement, Singapore, Energy and Buildings, 146, (2017), p27-37.
[https://doi.org/10.1016/j.enbuild.2017.03.071]

- 손흥구, 시계열 군집분석을 통한 단기 전력 수요 결합예측 기법 연구, 한국, 중앙대학교 박사학위논문, (2016), p16-17.Sohn, Hueng-goo, Electricity demand combined forecasting based on time series clustering analysis, Korea, Chung-Ang University, (2016), p16-17.
- Kanti Mardia, J. Kent, J. Bibby, Multivariate Analysis 1st Edition, (1979).
-
Jürgen Schmidhuber, Deep learning in neural networks: An overview, Switzerland, Neural Networks, 61, (2015), p85-117.
[https://doi.org/10.1016/j.neunet.2014.09.003]

-
Li, Jin-Yan, Yu, Ying-Lin, The estimation theory and optimization algorithm for the number of hidden units in the higher-order feed forward neural network, Hong Kong, Neural networks, 3, (1995), p1229-1233.
[https://doi.org/10.1109/ICNN.1995.487330]